Introduction
It is widely known that the uncertainty principle proposed by Heisenberg in 1927 [1] is one of the most elemental and important characteristics in the matter of quantum mechanics, which distinguishes from the classical counterpart. Canonically, the uncertainty principle suggests that one cannot accurately predict the momentum \(\hat {p}\) and position \(\hat {x}\) of a particle simultaneously. Later, Kennard [2] had proven and optimized the position-momentum uncertainty relation, and Robertson [3] further formulated the uncertainty principle via the standard deviation for two arbitrary incompatible observables \(\hat {R}\) and \(\hat {S}\) in the given system \(\hat {\rho }\), expressed as [4]
Apparently, the lower bound of Robertson’s relation depends on state as shown in Eq. (1). As a matter of fact, a trivial result, that the bound becomes zero, will take place if the systemic state is prepared in one of eigenstates of the two observables \(\hat {R}\) and \(\hat {S}\). With the advent of quantum information theory, Deutsch imposed Shannon entropy as an alternative measure of uncertainty and proposed the so-called entropic uncertainty relations (EURs) [5]. Technically, EUR is also regarded as the achievement of the combination of quantum mechanics and classical information theory. Noteworthily, Deutsch’s bound is only determined by the complementarity of the measured observables and is independent of the systemic state, eliminating the weakness of state dependence in Robertson’s relation. Moreover, Kraus [6] strengthened Deutsch’s result, whose result had been strictly verified by Maassen and Uffink [7]
where \(H(\hat {R})=-\sum _{i} {{p_{i}}{{\log }_{2}}{p_{i}}}\) represents the Shannon entropy and \({p_{i}} = \left \langle {\psi _{i}} \right |{\hat {\rho }}\left | {\psi _{i}} \right \rangle \). The maximal overlap \(c\left ({\hat {R},\hat {S}} \right) \equiv {\max _{j,k}}{\left | {\langle \psi _{j}|\phi _{k}\rangle } \right |^{2}}\) with |ψj〉 and |ϕk〉 respectively referring to the eigenvectors of \(\hat {R}\) and \(\hat {S}\). Due to the fact that \(c\left ({\hat {R},\hat {S}} \right)\) is correlated to the two observables themselves, it clearly demonstrates that the lower bound of EUR is state-independent.
Recently, quantum-memory-assisted entropic uncertainty relation (QMA-EUR) has been proposed by Renes et al. [8] and Berta et al. [9]
for a bipartite system AB. Where, \(S\left ({\hat {R}|B}\right)=S\left ({{\hat {\rho }_{\hat {R} B}}}\right)-S\left ({{\hat {\rho }_{B}}}\right)\) is denoted as the conditional von Neumann entropy [10, 11] of post-measurement states
with the 𝟙B is an identical operator in the Hilbert space of B. And \(S\left ({A|B} \right)=S\left ({{{\hat {\rho }}_{AB}}} \right) - S\left ({{{\hat {\rho }}_{B}}} \right)\) denotes the conditional von Neumann entropy of systemic density operator \({{\hat {\rho }}_{AB}}\). Following the inequality, one can attain some interesting points: (i) when A and B are disentangled, Maassen and Uffink’s result in Eq. (2) can be recovered from Eq. (3); (ii) when the measured particle A and the memory particle B are entangled, the bound can be reduced because that the conditional von Neumann entropy S(A|B) can be negative. Specifically, if A and particle B are maximally entangled, we have \(S\left ({\hat {R}|B} \right) + S\left ({\hat {S}|B} \right) \ge 0\) on account of S(A|B)=−log2d (d is the dimension of the measured particle), which reflects that Bob is able to predict perfectly Alice’s measured outcomes; (iii) if the quantum memory is absent, Eq. (3) becomes \(H\left (\hat {R}\right) + H\left (\hat {S}\right) \ge S\left ({\hat {\rho }}^{A} \right) - {\log _{2}}c\left ({\hat {R},\hat {S}} \right)\), which yields a tighter bound due to \(S\left ({\hat {\rho }}^{A} \right) \ge 0\).
As far as the QMA-EUR is concerned, it can be applied to a number of quantum tasks [12–18] including quantum teleportation [12], quantum key distribution [13], entanglement witness [9], quantum metrology [14, 15], quantum steering [16] and so forth. Additionally, some promising improvements had been made on QMA-EUR [19–35]. To be specific, by considering the second largest value of the overlap \(c(\hat {R},\hat {S})\), Coles and Piani [26] presented the uncertainty relation with a tighter bound. In 2015, Liu et al. [31] presented the uncertainty relation of multi-observable scenario. In 2016, Adabi et al. [32] optimized the lower bound by adding mutual information and Holevo quantity. Huang et al. [33] proposed a Holevo bound of QMA-EUR. More recently, Xie et al. [34] improved the lower bound of the entropic uncertainty relation for multiple measurements in bipartite systems. Until now, several groups have dedicated to make sustained progress in terms of experiments [36–43]. Note that, the tripartite EUR had been proposed by Renes and Boileau [44]
This inequality can be interpreted by the so-called monogamy game. Very recently, Ming et al. [45] put forward a tighter tripartite EUR
compared with Renes-Boileau’s result. Within the above,
with mutual information \({\mathcal {I}}\left ({A:B} \right) = S\left ({{{\hat {\rho }}^{A}}} \right) + S\left ({{{\hat {\rho }}^{B}}} \right) - S\left ({{{\hat {\rho }}^{AB}}} \right)\) and Holevo quantity \({\mathcal {I}}\left ({\hat {R}:B}\right)=S\left ({{{\hat {\rho }}^{B}}} \right) - \sum _{i} {{p_{i}}S\left ({{\hat {\rho }}_{i}^{B}} \right)} \). One performs measurement \(\hat {R}\) on particle A and obtains the i-th measurement outcome with probability \({p_{i}} = \text {Tr}_{AB}\left ({\Pi _{i}^{A}{{\hat {\rho }}^{AB}}\Pi _{i}^{A}} \right)\).
The above relations are suitable for issuing the cases in two or three-particle systems. While, the correlated many-body systems are usual and are frequently required to achieve the realistic quantum information processing, where the mentioned relations are ineffective. Especially, EUR takes an irreplaceable role in the security analysis of quantum key distribution within the multipartite setting. In this sense, we here would like to raise an open question: how to characterize the measurement uncertainty with respect to multipartite systems? Inspired by this, we will focus on addressing this issue in this article.
Generalized EUR
Theorem 1
In the case of multipartite systems, the generalized entropic uncertainty relation for multi-observable measurements can be described as
with
where \(\hat {\mathscr {O}}_{i}\) represents the i-th operator measured on subsystem A, and Bi denotes the i-th quantum memory other than particle A in multipartite system.
Proof
Based on the tripartite EUR expressed in Eq. (6), one can write m(m−1)/2 inequalities for m-observable measurements in (m+1)-party system \(\hat {\rho }_{A{B_{1}}{B_{2}{B_{3}}{B_{4}}\dots {B_{m}}}}\) as
□
Next, all these m(m−1)/2 inequalities are summed and both sides of the total inequality is divided by the quantity (m−1). As a consequence, we have
Likewise, by making use of Renes-Boileau’s result in Eq. (5), we rewrite it for m-observable measurement and (m+1)-party system \(\hat {\rho }_{A{B_{1}}{B_{2}{B_{3}}{B_{4}}\dots {B_{m}}}}\) and easily obtain
Comparing Eq. (11) with Eq. (12), we define
\(\Delta _{m} = -\frac { \sum \limits _{i < j, i,j=1}^{m} \log _{2}{c\left (\hat {\mathscr {O}}_{i},\hat {\mathscr {O}}_{j}\right)}}{m-1}+ mS\left ({\hat {\rho }}^{A} \right)-\sum \limits _{i}^{m} H({\mathscr {O}}_{i})-\sum \limits _{i}^{m} {\mathcal {I}}(A,B_{i})+\frac { \sum \limits _{i \neq j, i,j=1}^{m} {\mathcal {I}}\left (\hat {\mathscr {O}}_{i},B_{j}\right)}{m-1}\) and achieve the optimization of the two inequalities, i.e., taking the maximum between Δm and zero. We thereby obtain the expected generalized EUR for multi-observable in multipartite systems expressed as Eq. (8).
Examples
We have already obtained the generalized EUR for multi-observable in multipartite systems, and for the sake of illustrations, we here present some meaningful observables in practical quantum information processing. Assuming two groups of orthogonal bases {|ψa〉}a=1,2,…,d and {|ϕb〉}b=1,2,…,d are mutually unbiased bases (MUBs), |〈ψa|ϕb〉|2=1/d is satisfied by all a and b. For example, the typical two-dimensional Pauli measurements \(\mathbb {X},\mathbb {Y},\mathbb {Z} \) are regarded as perfect MUBs. If we adopt spin-1/2 Pauli matrices as the measured observables in several different 4-qubit systems \({\hat {\rho }}_{1234}, c\left (\hat {\mathscr {O}}_{i},\hat {\mathscr {O}}_{j}\right)\equiv 1/2\ (i\ne j)\) and thus \(-\log _{2}{c(\hat {\mathscr {O}}_{i}, \hat {\mathscr {O}}_{j})=1}\) naturally holds. Additionally, in order to compare our results with the previous, we generalize Renes-Boileau’s relation to the quadripartite framework
where
by virtue of Pauli measurement \(\mathbb {X},\mathbb {Y},\mathbb {Z}\), where
\(B_{MU1}=-\log _{2}{c(\mathbb {X},\mathbb {Y})}, B_{MU2}=-\log _{2} {c(\mathbb {X},\mathbb {Z})}, B_{MU3}=-\log _{2}{c(\mathbb {Y}, \mathbb {Z})}\). It is apparently that all is equal to 1, and \(\mathcal {B} =3/2\) is obtained.
In the following, one can apply our result to the case of three measurements, and obtain a tighter bound from the following relation
with
Now, we turn to compare our proposed bound with the previous derived from Renes-Boileau’s result in the case of different four-qubit state scenarios.
Mixed GHZ-type states
First of all, we take into account a type of mixed GHZ-type states. Generally, a four-qubit GHZ-type state can be written as
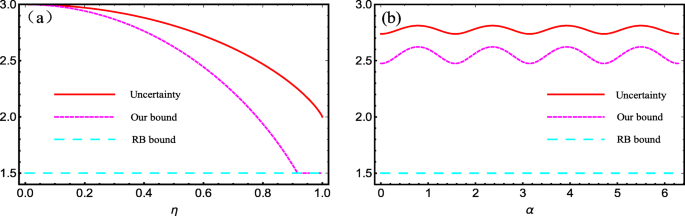
with the purity of the state η∈[0,1] and |GHZ〉= cosα|0000〉+ sinα|1111〉 with α∈[0,2π), and 𝟙16×16 denotes an identity 16×16 matrix. In this scenario, we plot the uncertainty, our bound and Renes-Boileau’s bound in Eq. (15) as Fig. 1a and b, with \(\alpha =\frac {\pi }{4}\) and η=0.5, respectively. It is straightforward to display that our derived bound is higher than Renes-Boileau’s one, i.e., URB≤UO≤U, which is reflecting that our bound outperforms the previous.
The entropic uncertainty and the lower bounds for mixed GHZ-type states. a Uncertainty and the lower bounds vs the state’s purity η. Red solid line denotes the quantity of the entropy-based uncertainty (left-hand side of Eq. (13)), magenta dashed line denotes our result (right-hand side of Eq. (15)) and cyan dashed line denotes Renes-Boileau’s result for four-qubit (right-hand side of Eq. (13)). b Uncertainty and the lower bounds vs the state’s parameter α. Red solid line denotes the quantity of the entropy-based uncertainty (left-hand side of Eq. (13)), magenta dashed line denotes our result (right-hand side of Eq. (15)) and cyan dashed line denotes Renes-Boileau’s result for four-qubit (right-hand side of Eq. (13))
W-type states
In addition, we proceed by considering a type of W-type four-qubit states, expressed as
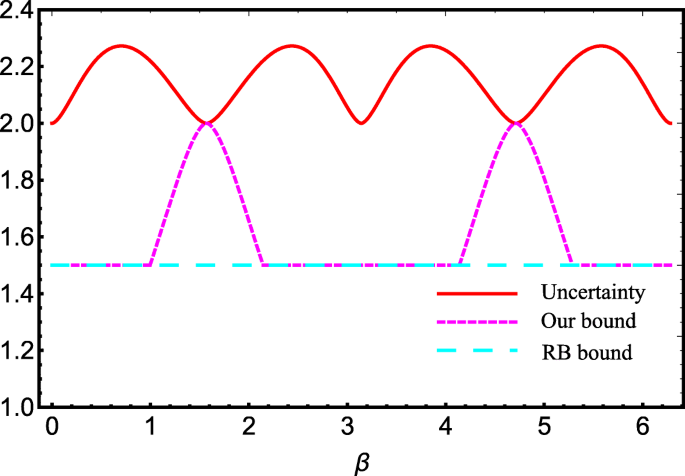
in the Hilbert space spanned by {|0〉,|1〉}, with β∈[0,2π). In this scenario, we have computed the uncertainty, our bound and Renes-Boileau’s result, which have been numerically indicated in Fig. 2. Following the figure, it is easy to realize that our bound is stronger than the previous one.
Uncertainty and the lower bounds vs the W-type state parameter β. Red solid line denotes the quantity of the entropy-based uncertainty (right-hand side of Eq. (13)), magenta dashed line denotes our result (right-hand side of Eq. (15)) and cyan dashed line denotes Renes-Boileau’s result for four-qubit (right-hand side of Eq. (13))
Random four-qubit states
To verify our obtained results, we consider more general states, i.e., arbitrary sets of random four-qubit states, which in principle contain both pure and mixed states. To begin with, let us introduce an effective approach to generate arbitrary random four-qubit states. Actually, arbitrary random four-qubit states can be expressed as the form of \(\hat {\rho }=\sum _{n=1}^{16}\lambda _{n}\left | \psi _{n} \right \rangle \left \langle \psi _{n} \right | \), where λn and |ψn〉 are regarded as the n-th eigenvalues and the eigenstates of \(\hat {\rho }\). Incidentally, the eigenvalue λn quantifies the probability that the systematic state \(\hat {\rho }\) is in the pure state |ψn〉. Next, one can set up an arbitrary unitary operation Θ by using the normalized eigenvector |ψn〉. An arbitrary four-qubit state also can be composed by arbitrary probabilities λn and arbitrary Θ. As a result, one can construct arbitrary four-qubit states by making use of the arbitrary set of probabilities and arbitrary unitary operation. In what follows, we utilize the random function ξ(x1,x2) to randomly generate a real number in a given interval [x1,x2]. Generally, one can generate random probabilities Pn by the following method
where i∈{1,2,3,…,15}.
Then a set of random probabilities λn (n∈{1,2,3,…,16}) is composed of Pm expressed as
Based on Eqs. (19) and (20), one can obtain a set of probabilities in descending order.
By way of constructing random unitary operation, we randomly generate one 16-order real matrix \( \mathcal {R} \) by the random function ξ(−1,1) with the given interval [−1,1]. Through using the real matrix \(\mathcal {R} \), a random Hermitian matrix is given by
where \(\mathcal {A}, \mathcal {B}\) and \(\mathcal {C}\) represent diagonal, strictly lower- and strictly upper-triangular part of the real matrix \(\mathcal {R}\), respectively, and \(\mathcal {B}^{T}\) represents the transposition of the matrix \(\mathcal {B}\).
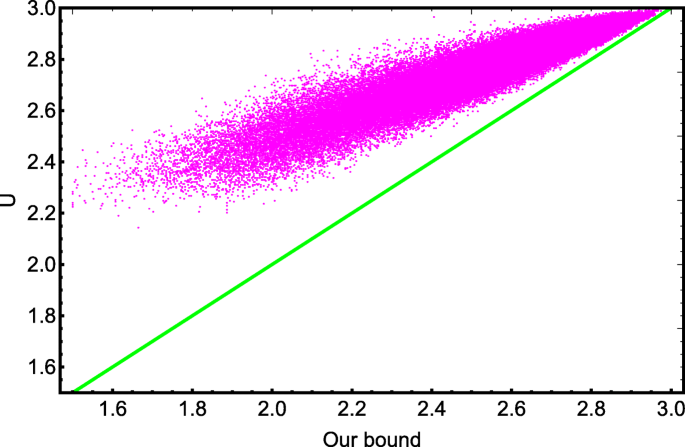
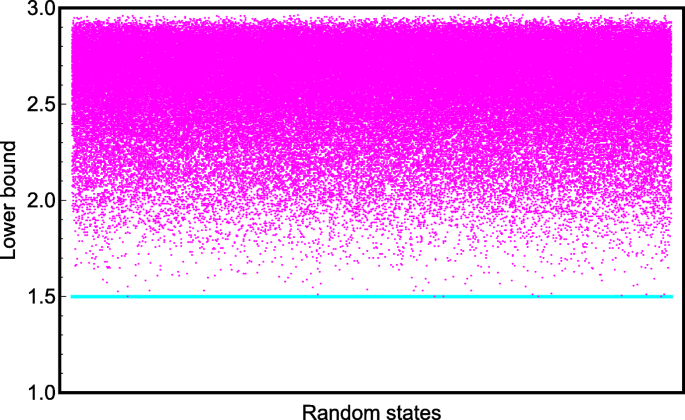
Following this calculation, one can get sixteen normalized eigenvectors |ψn〉 of the Hermitian matrix \( \mathcal {M}\), which forms the random unitary operation Θ. With the above procedures, one can perfectly construct random four-qubit quantum states by the expression \(\hat {\rho }=\sum _{n=1}^{16}\lambda _{n} \left | \psi _{n} \right \rangle \left \langle \psi _{n} \right | \). In order to testify our result, we take 1.5×105 random states to show the uncertainty and our bound as shown in Fig. 3. It is straightforward to demonstrate that the uncertainty U is great than or equal to the lower bound proposed by us, which also supports that our result is available for the arbitrary random states. In this sense, we claim that our result in Eq. (8) is universal. Moreover, we also compare our bound with Renes-Boileau’s bound with regard to randomly generated four-qubit states in Fig. 4. It is obvious that our bound is higher than Renes-Boileau’s bound, illustrating that our derived inequality is optimal.
Our lower bound in comparison with Renes-Boileau’s bound with respect to 1.5×105 four-qubit random states. The X-axis is denoted as randomly generated four-qubit states, and the Y-axis denotes the magnitude of our lower bound in Eq. (15), and the cyan line represents Renes-Boileau’s bound in Eq. (13)
Conclusions
To summarize, we have derived general entropic uncertainty relations for multiple-observable measurements in multipartite correlated systems, which is essentially deemed as a universal architecture in quantum information theories. Herein, we employ three two-dimensional Pauli measurement \(\mathbb {X}, \mathbb {Y}\), and \(\mathbb {Z}\) as the incompatibility in the framework of arbitrary four-qubit systems, including GHZ-type states, W-type states and random four-qubit states. It turns out that our derived bound is tighter than Renes-Boileau’s one, which shows that our generalized EUR is optimal. In this regard, it is believed that our result will be instrumental in various measurement-based quantum information processing, especially quantum precision measurements [34] and improving quantum secret key rate [46] in multipartite systems. Hence, we argue that our explorations would pave the avenue on quantum measurement estimation for multiple observables within many-body systems in the area of quantum information science.