Introduction
The spin-orbital-angular-momentum (SOAM) coupling, the coupling between the spin degree of freedom and the external orbital motion, is one of the most common phenomena in our nature. A prominent example in classical physics is the astronomical fact that the Moon always shows the same side to the Earth, known as the tidal locking or the spin-orbit locking [1]. In atomic physics, SOAM coupling is a relativistic effect, which gives rise to the fine structure of energy levels of hydrogen atoms [2]. A similar effect occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model [3]. In condensed-matter physics, an analogous coupling between the electron spin and its velocity, namely the spin-linear-momentum (SLM) coupling or spin-orbit (SO) coupling, results in a variety of intriguing and fundamental phenomena, such as the spin-Hall effect or topological insulators [4], which have potential applications in quantum devices. Although numerous fascinating behaviors of many-body quantum systems are closely related to SOAM or SO coupling, they are mostly intractable or manifest themselves under extreme conditions. Therefore, it is of important significance to find a system, which could mimic the unique features of SOAM- or SO-coupled quantum systems in a controllable way.
Owing to the advances in the experimental technique, ultracold atomic gases acquire a high degree of controllability and tunability in interatomic interaction, geometry, purity, atomic species, and lattice constant (of optical lattices) [5,6,7,8,9]. To date, ultracold quantum gases have emerged as a versatile platform for exploring a broad variety of many-body phenomena and can realize physical effects with analogs throughout physics [4, 10, 11]. However, unlike charged particles, neutral atoms cannot experience the influence of external electromagnetic fields. Fortunately, thanks to the controlling of atom-light interaction, the internal hyperfine states of neutral atoms, playing a role of (pseudo-)spin, are coupled to their linear momentum of center-of-mass motion, which equivalently introduces a class of SO couplings experienced by atoms. For example, the theoretical scheme of realizing a one-dimensional (1D) SO coupling with equal Rashba and Dresselhaus strengths was proposed in cold atoms according to a Raman process with a simple \(\Lambda\)-type configuration [12]. Then, the basic idea was broadly applied in experiments with both bosonic and fermionic atoms [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Soon, an impressive amount of theoretical and experimental efforts have been devoted to the realization of high-dimensional SO coupling [28,29,30,31,32,33,34,35,36,37,38,39,40,41]. The high-dimensional SO coupling corresponds to a non-Abelian gauge field and has nontrivial geometric or topological effects, which are absent in systems with 1D SO coupling. Regarding the controllability of ultracold quantum gases, it opens a new era, from the quantum simulation point of view, to study the fundamental physics resulting from SO-coupling as well as newly emergent quantum phases [42,43,44].
Though the SO coupling has intensively been studied in the field of condensed matter as well as in ultracold atoms, it is different from the original meaning of SO coupling in atomic physics, in which it indicates the coupling between the spin and the orbital angular momentum. Recently, such type of SO coupling, i.e., the SOAM coupling, is theoretically proposed in cold atoms and enriches our understanding of quantum many-body physics [45,46,47,48,49,50,51,52]. It is experimentally achieved in \(^{87}\)Rb Bose gases according to a Raman process by using a pair of copropagating laser beams operated in Laguerre-Gaussian (LG) modes [53,54,55]. The ground-state phase diagram of the systems is confirmed. The hysteresis loop is observed across the phase boundary, which is a hallmark of the first-order phase transitions. This is due to the unique property of the quantized angular momentum, unlike that of the linear momentum in SLM-coupled systems [56,57,58,59]. Later on, a considerable amount of attention has been paid to a supersolid-like phase [60,61,62,63,64], namely the angular stripe phase, which breaks the U(1) gauge symmetry to behave like a superfluid and also breaks the angular translational symmetry (or the rotational symmetry) to manifest spatial order in the angular density [65]. Nevertheless, this kind of angular stripe phases has not yet been observed because of the narrow window of parameters that is hardly reached in experiments at present [63].
Soon, the idea of SOAM coupling is theoretically generalized to fermionic systems [66, 67], where the pairing mechanics plays a crucial role in the Fermi superfluid. While it is shown that the SOAM coupling leads to the spin-dependent vortex formation in Bose-Einstein condensates, SOAM coupling alone does not induce vortices in a Fermi superfluid, since fermions in a Cooper pair would acquire opposite orbital angular momenta that cancel each other, yielding a superfluid devoid of vortices. However, by introducing a moderate detuning away from the two-photon resonance in the Raman process, which breaks the time-reversal symmetry of systems, a giant vortex superfluid phase could remain stable in SOAM-coupled Fermi gases. The Cooper pairs can possess quantized angular momenta, featured as an angular analog of the Fulde-Ferrell pairing state in SO-coupled Fermi gases, where Cooper pairs inevitably carry finite center-of-mass momentum due to the asymmetry of SO-dressed Fermi surface under Zeeman field [68,69,70,71,72,73,74]. These SOAM-coupling induced vortices have fascinating and unique features. For example, their size could be as strikingly large as the length scale comparable to the waist of Raman beams. This is markedly different from previously studied vortices in atomic Fermi superfluids, where changes in the vortex-core structure predominantly take place within a short-length scale set by the interatomic separation [75, 76]. Besides, the vortex core exhibits a large spin imbalance, which originates from spin-polarized vortex-bound states, or the so-called Caroli–de Gennes–Matricon (CdGM) states [77], and would serve as an ideal experimental signal. Subsequently, the topological characters of a ring-shape SOAM-coupled Fermi superfluid are explored, in which the ac-stark potential of Raman beams provides a strong radial confinement [78]. The genic features of topological superfluid are encoded in the quantized angular degree of freedom. Nevertheless, a fundamental hurdle to the experimental observation of the SOAM-coupling-induced pairing states is the inevitable heating during the Raman process, which makes it difficult to cool the system below the superfluid transition temperature. Instead, it is reasonable to expect that molecule states in the SOAM-coupled Fermi gases could survive even above the critical temperature, as what occurs in SO-coupled systems [19, 79]. Accordingly, a scenario, using the radio-frequency spectroscopy based on two-body physics, provides an accessible detection of the pairing mechanics under current experimental conditions [80].
The rest of the review is arranged as follows. In the next section, we present the theoretical scheme of how the SOAM-coupling effect could be achieved in cold atoms according to a Raman transition. Starting from a semiclassical description of atom-light interaction, the effective Hamiltonian of a single atom is derived. The possible symmetries of the system are then discussed, which play an important role in understanding the fundamental properties of the system. In Section 3, single-particle physics is introduced, including the energy spectrum and the intriguing spin texture of the ground state. The emergent synthetic gauge field experienced by cold atoms in the presence of atom-light interaction is also demonstrated. In Section 4, the ground-state properties of weakly interacting SOAM-coupled Bose gases are discussed, based on the solution of the Gross-Pitaevskii equation. The quantum phases of Bose condensates are then identified as well. The emphasis on the properties of the angular stripe phases is presented. We also propose possible scenarios to enlarge the window of parameters that might be accessible in experiments to observe them. It follows the discussion on the ground state of interacting SOAM-coupled Fermi gases in Section 5. The pairing mechanism of fermions in the presence of SOAM-coupling is introduced. Two exotic pairing states, i.e., SOAM-coupling-induced giant vortex and topological superfluid states, are shown to be stabilized under SOAM coupling. Subsequently, the most recent progress of experiments related to SOAM-coupled quantum gases is summarized in Section 6. Section 7 is devoted to the conclusions and outlooks for future advances.
Spin-orbital-angular-momentum coupling
The key idea of generating SOAM coupling in neutral atoms has been proposed by several earlier works [46,47,48], in which two hyperfine states of atoms are coupled by a pair of copropagating LG beams according to a Raman process as shown in Fig. 1. The two LG beams carry different orbital angular momenta along the direction of beam propagation that leads to an orbital angular momentum change of atoms when transitioning between the two ground hyperfine states. In the following, we are going to derive the effective Hamiltonian of an alkali metal atom in the presence of a pair of Raman LG beams based on the semiclassical description of atom-light interaction [45, 81, 82].
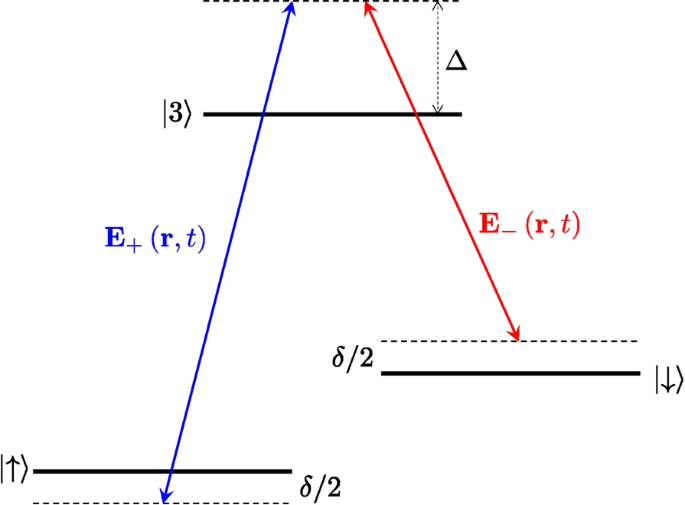
Scheme of the SOAM coupling. Two hyperfine states of atoms (denoted by \(\left| \uparrow \right\rangle\) and \(\left| \downarrow \right\rangle\)) are coupled to an excited state \(\left| 3\right\rangle\) by a pair of far-detuned copropagating Laguerre-Gaussian beams \(\mathbf {E}_{\pm }\left( \mathbf {r},t\right)\). Here, \(\delta\) and \(\Delta\) are the two-photon and single-photon detunings respectively
Semiclassical theory of atom-light interactions
In the semiclassical theory, the atom-light interaction during the Raman process is described by the following Hamiltonian
in the bare hyperfine basis \(\left[ \left| \uparrow \right\rangle ,\left| \downarrow \right\rangle ,\left| 3\right\rangle \right] ^{T}\), where \(\hbar \omega _{\sigma }\) (\(\sigma =\uparrow ,\downarrow ,3\)) is the bare energy of atoms in different hyperfine states, and \(V_{\sigma \sigma ^{\prime }}=-\left\langle \sigma \right| \mathbf {d}\cdot \mathbf {E}_{(\pm )}\left| \sigma ^{\prime }\right\rangle\) characterizes the dipole interactions between the valence electron and light fields. Here, \(\mathbf {d}\) is the electric moment of the valence electron and
are the electric fields experienced by atoms, where \(\hat{\mathbf {e}}_{\pm }\) denote the unit vectors of the polarization direction of light, \(\omega _{\pm }\) are the angular frequencies of Raman beams, and \(\mathcal {E}_{\pm }\left( \mathbf {r}\right)\) are the spatial complex amplitudes. The wave function of atoms can also be written in the bare hyperfine basis as
and \(\eta _{\sigma }\) are arbitrary factors that are chosen for later convenience. Inserting Eqs. (1) and (3) into the Schrödinger equation \(i\hbar \partial _{t}\Psi =\hat{H}_{al}\Psi\) and by choosing
we easily obtain
under the rotating-wave approximation (RWA) [81], where \(\rho _{+}\equiv \left\langle 3\right| -\mathbf {d}\cdot \hat{\mathbf {e}}_{+}\left| \uparrow \right\rangle\) and \(\rho _{-}\equiv \left\langle 3\right| -\mathbf {d}\cdot \hat{\mathbf {e}}_{-}\left| \downarrow \right\rangle\) are the matrix elements of the electric dipole moments, and \(\delta /\hbar \equiv \left( \omega _{+}-\omega _{-}\right) -\left( \omega _{\downarrow }-\omega _{\uparrow }\right)\) and \(\Delta /\hbar \equiv \left( \omega _{+}+\omega _{-}\right) /2-\left[ \omega _{3}-\left( \omega _{\uparrow }+\omega _{\downarrow }\right) /2\right]\) are respectively the two-photon and single-photon detunings. When the excited state \(\left| 3\right\rangle\) is far from the resonance, we may adiabatically eliminate it by setting \(\partial _{t}c_{3}\left( t\right) =0\), and then Eq. (9) yields
After inserting Eq. (10) into Eqs. (7) and (8), we arrive at
where
are respectively the diagonal and off-diagonal ac-stark shifts. We find that the diagonal ac-stark shift \(\chi _{\pm }\left( \mathbf {r}\right)\) provides an effective trapping potential for atoms that could be removed by properly choosing a tune-out wavelength of LG beams in the experiment [55, 83, 84]. The off-diagonal ac-stark shift \(\Omega \left( \mathbf {r}\right)\) leads to a space-dependent coupling between two hyperfine states \(\left| \uparrow \right\rangle\) and \(\left| \downarrow \right\rangle\), and then results in a SOAM coupling of atoms as we will see below.
SOAM-coupled Hamiltonian and symmetries
Without loss of generality, we consider a two-dimensional (2D) configuration for simplicity in that atoms are confined in the \(z=0\) plane, and the pair of Raman LG beams copropagate along the \(-{\mathbfit{z}}\) direction with the spatial complex amplitude
where \(I_{0}\) and w are respectively the intensity and waist of the beams, and \(l_{\pm }\) are their winding numbers. Here, we have adopted a polar coordinate \(\mathbf {r}=\left( r,\varphi \right)\). Consequently, the single-atom Hamiltonian in the presence of Raman LG beams takes an effective form of
with
where \(V_{ext}\left( r\right) =m\omega ^{2}r^{2}/2\) is the external harmonic potential, \(n=\left( l_{+}-l_{-}\right) /2\) is the angular momentum transferred to atoms, and \(\Omega \left( r\right) \equiv \Omega _{R}\left( r/w\right) ^{\left| l_{+}\right| +\left| l_{-}\right| }e^{-2r^{2}/w^{2}}\), with the coupling strength \(\Omega _{R}=\left| \rho _{+}^{*}\rho _{-}\right| I_{0}/2\Delta\), is the radial Rabi frequency. Here, we have assumed \(\chi _{+}\left( r\right) =\chi _{-}\left( r\right) \equiv \chi \left( r\right)\) for simplicity, which is only dependent on \(\left| \mathbf {r}\right| =r\). Besides, we also discard the internal phase difference between the matrix elements of electric dipole moments \(\rho _{+}\) and \(\rho _{-}\) that is irrelevant to the problem.
Let us then analyze the possible symmetries of the single-atom Hamiltonian (15). It is obvious that the rotational symmetry with respect to the z axis is broken by the dependence of Raman coupling \(\hat{H}_{so}\) on the azimuthal angle \(\varphi\). The orbital angular momentum of the atom is thus no longer conserved, since it follows a change of orbital angular momentum accompanied by the spin flip in the Raman process [46, 60, 62]. By introducing a unitary transformation \(\hat{U}=\exp \left( in\varphi \hat{\sigma }_{z}\right)\), the single-atom Hamiltonian becomes \(\hat{\mathcal {H}}_{0}=\hat{U}\hat{H}_{0}\hat{U}^{\dagger }\), i.e.,
where \(\hat{L}_{z}=-i\hbar \partial /\partial \varphi\), and \(\hat{\sigma }_{x,z}\) are Pauli matrices. We find that the angular momentum \(\hat{L}_{z}\) commutes with the single-atom Hamiltonian \(\hat{\mathcal {H}}_{0}\) under the unitary transformation \(\hat{U}\), and thus \(\hat{L}_{z}\) is conserved. Therefore, the original single-atom Hamiltonian \(\hat{H}_{0}\) demonstrates the symmetry under the redefined rotational transformation \(\hat{\mathcal {R}}\left( \varphi \right) \equiv \hat{U}^{\dagger }e^{-i\hat{L}_{z}\varphi /\hbar }\hat{U}\). Then, \(\hat{L}_{z}\) may be regarded as the operator of quasi-angular momentum (QAM), and each eigenstate of the system possesses definite values of QAM characterized by the corresponding quantum number \(l_{z}\). It is related to the angular momentum of each spin component in the laboratory frame by \(l_{\uparrow ,\downarrow }=l_{z}\mp n\). Here, we find that the term of \(\hat{L}_{z}\hat{\sigma }_{z}\) appears, which characterizes the crucial SOAM-coupling effect that is well familiar to us in atomic physics.
At the resonance of Raman coupling with \(\delta =0\), the system demonstrates an additional symmetry, namely the time-reversal symmetry. The single-atom Hamiltonian \(\hat{H}_{0}\) commutes with the time-reversal operator \(\hat{T}=\hat{\sigma }_{x}\hat{K}\), and thus is invariant under the time-reversal transformation, where \(\hat{K}\) denotes the operator of complex conjugation [46, 62]. This symmetry may be translated into a QAM frame as \(\hat{\mathcal {T}}=\hat{U}\hat{T}\hat{U}^{\dagger }\), and then we have \(\left[ \hat{\mathcal {T}},\hat{\mathcal {H}}_{0}\right] =0\). The time-reversal symmetry guarantees that the spectrum of a single atom is symmetric about the QAM \(l_{z}=n\).
Single-particle physics
Single-particle spectrum
Regarding the rotational symmetry of the single-atom Hamiltonian (17), each eigenstate of a single atom should possess a definite QAM \(l_{z}\), whose wave function may be written as
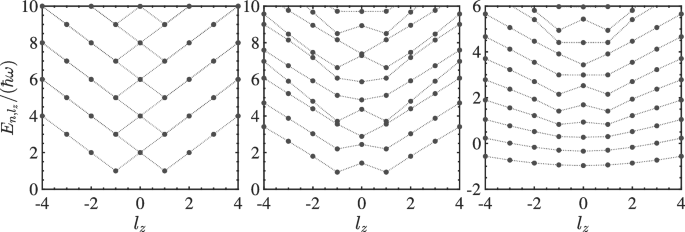
Then, the Schrödinger equation \(\hat{\mathcal {H}}_{0}\Psi _{l_{z}}\left( \mathbf {r}\right) =E\Psi _{l_{z}}\left( \mathbf {r}\right)\) reduces to two coupled one-dimensional radial equations of \(\psi _{\uparrow ,\downarrow }\left( r\right)\), which are easily solved by using the finite-difference method [46]. The single-particle dispersion relations between the energy E and QAM \(l_{z}\) are shown in Fig. 2 for three typical coupling strengths. Here, the winding numbers of two Raman beams are respectively chosen to be \(l_{+}=-2\) and \(l_{-}=0\), and we consider the situation at the two-photon resonance with \(\delta =0\). The symmetry of the single-particle dispersion about \(l_{z}=0\) is guaranteed by the time-reversal symmetry \(\hat{\mathcal {T}}\) discussed above. This means that the Schrödinger equation is invariant under the exchange of the spin indices, which sends \(n\rightarrow -n\) as well.
The single-particle dispersion for three typical SOAM-coupling strength \(\Omega _{R}/\hbar \omega =0\), 100 and 250 (left to right). The energy is characterized by two quantum numbers, i.e., the radial quantum number or band index n and the quasi angular momentum \(l_{z}\). Here, we have set the two-photon detuning \(\delta =0\) and the off-diagonal ac-stark shift \(\chi \left( r\right)\)=0 as well
In the absence of SOAM coupling, i.e., \(\Omega _{R}=0\), the energy band structure is simply that of the spinor harmonic oscillator with the excitation interval \(\hbar \omega\). The ground state is characterized by the QAM \(l_{z}=\pm 1\), which is doubly degenerate. The angular momentum for each spin component in the laboratory frame is \(\left( l_{\uparrow },l_{\downarrow }\right) =\left( 0,-2\right)\) and \(\left( l_{\uparrow },l_{\downarrow }\right) =\left( 2,0\right)\) corresponding to the QAM \(l_{z}=-1\) and 1, respectively. As the SOAM-coupling strength \(\Omega _{R}\) gradually increases, the spin is no longer a good quantum number, and small amounts of atoms are transferred into the previously vacant spin component, while the ground state still has the twofold degeneracy with definite QAM. By further increasing the coupling strength, the system finally jumps into the QAM \(l_{z}=0\) ground state, which gives rise to a first-order phase transition to a spin-balanced population [55]. This is due to the unique property of the quantized angular momentum in SOAM-coupled systems. In SLM-coupled systems, such phase transition is a continuous type, where the doubly degenerate ground states finally merge into each other as the Raman-coupling strength increases [56,57,58,59].
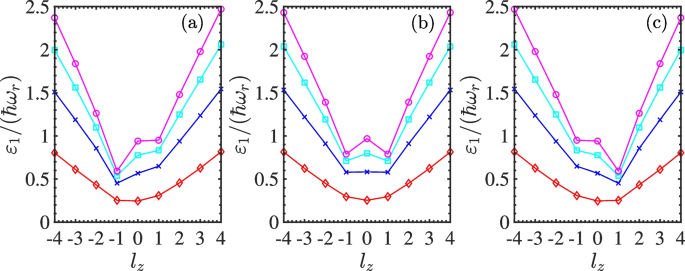
Let us look closely at the evolution of the lowest-energy band as presented in Fig. 3 at different coupling strengths. Its symmetry about \(l_{z}=0\) is preserved by the time-reversal symmetry at the two-photon resonance \(\delta =0\) as shown in Fig. 3(b). We demonstrate how the ground state evolves from the doubly degenerate states (\(l_{z}=\pm 1\)) into a single one (\(l_{z}=0\)) as the coupling strength increases. However, away from the two-photon resonance with \(\delta \ne 0\), we find that the degeneracy of the ground states at weak coupling strength is lifted, since the time-reversal symmetry is broken by the two-photon detuning (as shown in Fig. 3(a) and (c)). The ground state is located either at \(l_{z}=-1\) or 1 determined by the sign of the two-photon detuning. This gives rise to an additional first-order phase transition by continuously varying the two-photon detuning [55]. At strong coupling strength, the system again jumps into the QAM \(l_{z}=0\) ground state as we discussed above.
Lowest energy band in the single-particle dispersion at a negative, b zero, and c positive two-photon detuning \(\delta\) when the SOAM-coupling strength \(\Omega _{R}\) increases (top to bottom). Adapted from Ref. [60]
Spin textures
The SO coupling gives rise to intriguing spin textures. For example, it has been found in studies of 2D Rashba SO-coupled BECs [85, 86] and BECs exposed to LG beams [87] that the spin texture contains a topological knot known as a 2D skyrmion. It is one kind of topological defects protected by their topological nontriviality. Regarding the spin texture of SOAM-coupled systems, it is useful to define a spin vector [46, 85, 86]
with the spin operator \(\hat{\mathbf {s}}=\left( \hbar /2\right) \left( \hat{\sigma }_{x},\hat{\sigma }_{y},\hat{\sigma }_{z}\right)\). The skyrmion number defined as
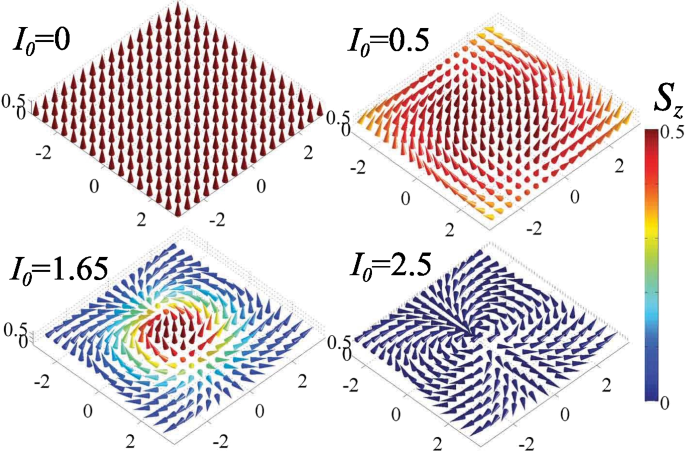
is a measure of the winding of the spin texture, which distinguishes a skyrmion texture from that of the vacuum. If it equals 1 or \(-1\), a topological knot exists in the spin texture [88, 89]. The ground-state spin texture at four typical coupling strengths is presented in Fig. 4. At weak coupling strength, the twofold degenerate ground state gives rise to a spin texture corresponding to a half skyrmion. As the coupling strength increases, the ground state finally jumps to the QAM \(l_{z}=0\) state. The system reaches a spin-balanced state, which does not support a skyrmion texture. The local spin becomes planar and lies in the \(x-y\) plane, and thus the skyrmion number vanishes.
Spin texture of the ground state of a SOAM-coupled system at different coupling strengths. The arrows point in the direction of the local spin \(\mathbf {S}\), and the color represents the projection of the spin onto the z axis. The figure is adapted from Ref. [46], as well as corresponding parameters therein
Artificial gauge field
In the following, we are going to demonstrate how the artificial (synthetic) gauge field may emerge for neutral atoms in the presence of atom-light interactions. It is one of the essential ingredients for the simulation of charged particles moving in the electromagnetic field by using cold atoms [10, 90,91,92,93], which gives rise to a series of intriguing phenomena, such as the spin Hall effect [94,95,96]. To this end, we may simply rewrite the atom-light Hamiltonian (16) in an explicit form of
with the effective Zeeman field
We find easily that the Raman-induced atom-light interaction effectively provides a spin-magnetic interaction equivalent to that for a spin-half charged particle in a space-dependent Zeeman field \(\mathbf {Z}\left( \mathbf {r}\right)\). The diagonalization of \(\hat{H}_{so}\) simply gives the dressed spin states [10], i.e.,
with eigenvalues \(\pm \hbar \left| \mathbf {Z}\left( \mathbf {r}\right) \right| /2\), respectively, and \(\tan \phi =\tan 2n\varphi\) and \(\tan \theta =2\Omega \left( r\right) /\delta\), which determine the orientation of the effective Zeeman field. It is obvious that \(\left| \zeta _{\pm }\right\rangle\) denotes the states that the pseudo-spin of the atom aligns along or inversely to the direction of the local Zeeman field. In the following, let us consider the atom moves slowly in the space-dependent Zeeman field \(\mathbf {Z}\left( \mathbf {r}\right)\), and its pseudo-spin follows adiabatically one of the eigenstates of \(\hat{H}_{so}\), namely for example \(\left| \zeta _{+}\right\rangle\). Then, the full wave function of the atom can be written as \(\left| \Psi \left( \mathbf {r},t\right) \right\rangle =\psi _{+}\left( \mathbf {r},t\right) \left| \zeta _{+}\right\rangle\), the evolution of which is governed by the Schrödinger equation \(i\hbar \partial _{t}\left| \Psi \left( \mathbf {r},t\right) \right\rangle =\hat{H}_{0}\left| \Psi \left( \mathbf {r},t\right) \right\rangle\) under the Hamiltonian (15). Here, \(\psi _{+}\left( \mathbf {r},t\right)\) is the spatial wave function characterizing the center-of-mass motion of the atom in the internal dressed state \(\left| \zeta _{+}\right\rangle\). By projecting the Schrödinger equation onto the internal dressed state \(\left| \zeta _{+}\right\rangle\), we obtain easily
Two geometric potentials \(\mathbf {A}\) and W emerge in addition to the external trapping potential \(V_{ext}\) and Zeeman energy \(\hbar \left| \mathbf {Z}\right| /2\), which are respectively the vector potential [10]
and the scalar potential
It is obvious that Eq. (24) takes the same form as that for a spin-half particle with a unit charge (\(q=1\)) [2]. The effective magnetic field \(\mathbf {B}\left( \mathbf {r}\right)\) associated with \(\mathbf {A}\left( \mathbf {r}\right)\) is
Here, we should pay special attention to the difference between the Zeeman field \(\mathbf {Z}\left( \mathbf {r}\right)\) and the effective magnetic field \(\mathbf {B}\left( \mathbf {r}\right)\): the Zeeman field \(\mathbf {Z}\left( \mathbf {r}\right)\) only lifts the degeneracy of the bare spin states and does not affect the center-of-mass motion of the atom, while \(\mathbf {B}\left( \mathbf {r}\right)\) is the magnetic field experienced by the center-of-mass motion of the atom when it moves in the presence of the atom-light interaction and keeps staying in the internal dressed state \(\left| \zeta _{+}\right\rangle\). In the presence of Raman LG beams, the effective magnetic field \(\mathbf {B}\left( \mathbf {r}\right)\) takes the explicit form of
which is perpendicular to the \(x-y\) plane and along the z axis.
SOAM-coupled Bose gases
The interatomic interaction plays a crucial role in interacting many-body quantum systems. In this section, we are going to introduce the ground-state quantum phases of weakly-interacting Bose-Einstein condensates (BECs) in the presence of SOAM coupling, within the framework of the mean-field theory based on the Gross-Pitaevskii (GP) equation. The interaction gives rise to the appearance of a variety of intriguing angular stripe phases, which have not yet been observed in current experiments. The possible theoretical scheme is proposed for observing angular stripe phases in the \(^{41}\)K atomic gas with tunable interatomic interactions.
The mean-field Hamiltonian of a weakly interacting Bose gas in the presence of SOAM coupling takes the form of
where \(\hat{\mathcal {H}}_{0}\) is the single-particle Hamiltonian (17), \(\Psi \left( \mathbf{{r}}\right) \equiv \begin{bmatrix}\Psi _{\uparrow }\left( \mathbf{{r}}\right) ,\Psi _{\downarrow }\left( \mathbf{{r}}\right) \end{bmatrix}^T\) is the spinor wave function for the condensate, and \(g_{\sigma \sigma '}\) is the effective 2D intra- (\(\sigma =\sigma '\)) and inter-species (\(\sigma \ne \sigma '\)) interaction strength.
Gross-Pitaevskii theory and a variational approach
When the interaction is taken into account, the nonlinearity may spontaneously break the rotational symmetry of the system. We can no longer assume that the condensate possesses the definite QAM \(l_{z}\). The ground-state solution of the GP equation is first attempted by using a split-step imaginary time evolution [46]. Three kinds of quantum phases are identified: two of them still preserve the rotational symmetry as the many-body analogs of the single-particle ground state, while the third one is a newly emergent angular stripe phase, which does not possess a definite QAM and breaks the rotational symmetry.
Therefore, apart from the angular stripe phase, one may take the states with a definite QAM for the condensates as a good starting point when taking into account interactions. If the system or the condensate wave function preserves the axial symmetry, one may consider the QAM \(l_{z}\) as a good quantum number and adopt the Ansatz for the condensate [60]
with the radial wave function \(f_{_{l_{z}\sigma }}\), and substitute it into the GP equation,
where \(\mu\) is the chemical potential, and the diagonal element takes the form of \(\mathcal {L}_{\sigma }\equiv g_{\sigma \sigma }n_{\sigma }+g_{_{\uparrow \downarrow }}n_{\bar{\sigma }}\) (spin index \(\sigma \ne \bar{\sigma }\)). Thus, one can then determine the ground-state wave function \(\psi _{_{l_{z}}}\) of the rotationally symmetric phases at zero temperature by solving self-consistently this GP equation.
Nonetheless, to capture the exotic angular stripe phase that does not possess a definite QAM, a variational Ansatz with various angular momenta is adopted for the condensate wave function in determining the ground state with an energy-minimizing method [60].
In the realistic configuration of recent experiments [53, 55], the orbital angular momentum transferred by the LG lasers is \(n=\pm 1\), giving rise to minima with the QAM located at \(l_z=\pm 1\), or 0 in the single-particle dispersion. Thus, the adopted variational Ansatz could be taken as
with real weighting coefficients \(\alpha , \beta , \gamma\) and the associated phases \(\theta _{\alpha }\), \(\theta _{\beta }\), and \(\theta _{\gamma }\). In general, \(\psi _{_{l_{z}}}\) is the state with a definite QAM \(l_{z}\), which can either be the single-particle state or the one obtained by self-consistently solving the GP equation (31) when the interaction is taken into account. Nonetheless, the latter is adopted here which contributes a lower mean-field energy than the one from the single-particle states particularly at low Rabi frequencies or at relatively strong interactions [60]. Therefore, the ground-state wave function \(\Psi \left( \mathbf {r}\right)\) is then determined from the minimization of the mean-field energy in Eq. (29) with respect to the variational parameters. It is worth mentioning that, three definite-QAM states are merely sufficient here, regarding the recent experimental configuration with the transferred orbital angular momentum \(n=\pm 1\) [55]. One may need more definite-QAM states in the variational Ansatz for larger n.
Typical ground-state phases
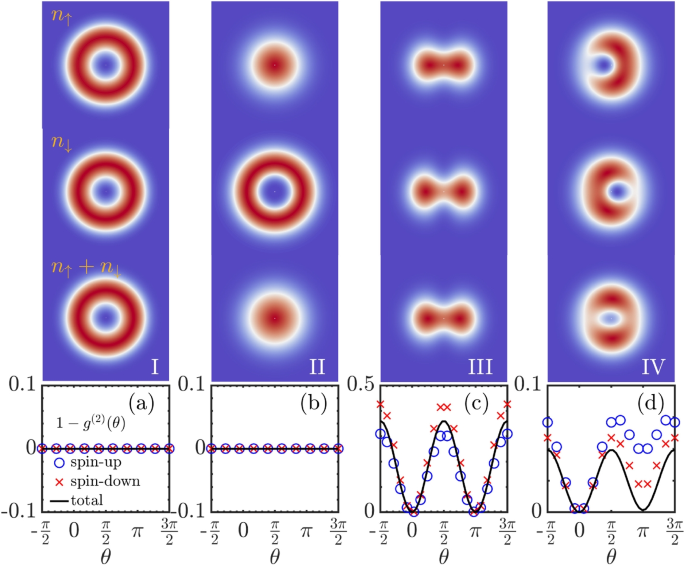
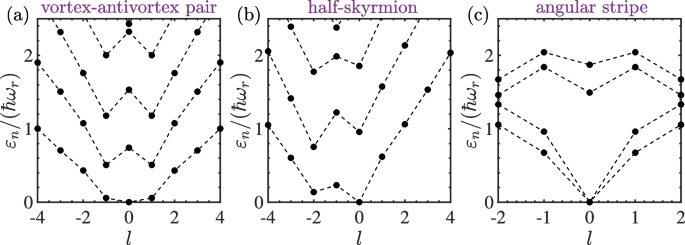
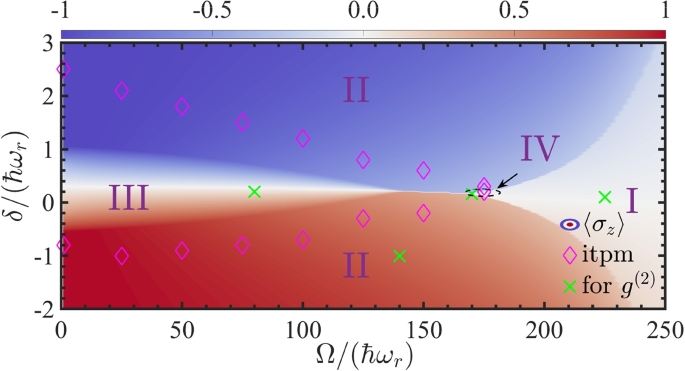
After solving self-consistently the GP equation in Eq. (31) and minimizing the total energy in Eq. (29) with a constructed variational Ansatz, the ground-state wave function \(\Psi (\mathbf {r})\) can then be calculated and the phase diagram at zero temperature is conveniently depicted for a weakly-interacting SOAM-coupled Bose gas [60]. In general, four distinct phases can be identified in the parameter space of \(g_{\sigma \sigma '}\) and \(\Omega\) at a vanishing two-photon detuning \(\delta =0\). The first is the vortex-antivortex pair phase which behaves as a vortex, as shown by the first column in Fig. 5. It locates at zero QAM \(l_{z}=0\) (i.e., \(\beta =1, \alpha =\gamma =0\)) with zero magnetization \(\langle \sigma _{z}\rangle =0\) and \(\langle \sigma _{x}\rangle =-1\). The second one is the half-skyrmion phase with two spin-component densities being a Thomas-Fermi-like distribution and a vortex (see the second column in Fig. 5). This phase is magnetic, i.e., \(\langle \sigma _{z}\rangle \ne 0\) and \(\langle \sigma _{x}\rangle \ne 0\), with a definite QAM at \(l_{z}=-1\) or 1 (i.e., \(\alpha =1, \beta =\gamma =0\) or \(\gamma =1, \alpha =\beta =0\)). The third and fourth ones are called angular stripe phases shown by the peanut-like and halo-like density profiles in the last two columns of Fig. 5. Both of them have no definite \(l_{z}\) with \(\alpha =\gamma =1/\sqrt{2},\beta =0\) or \(\alpha =\gamma \ne 0,\beta \ne 0\), and they have no magnetization \(\langle \sigma _{z}\rangle =0\) and \(\langle \sigma _{x}\rangle \ne 0\). In addition, one can further investigate the elementary excitation spectrum to distinguish these phases and then characterize the phase transitions. The spectrum of a SOAM-coupled Bose gas is discrete due to the quantized angular momentum. In detail, the vortex-antivortex pair phase possesses a symmetric spectrum with a single phonon mode, see Fig. 6a. However, the half-skyrmion phase breaks spontaneously the double degeneracy in the single-particle dispersion and thus has an excitation spectrum with a discrete roton-maxon structure [60], as shown in Fig. 6b. Most interestingly, owing to the spontaneous breaking of both the U(1) gauge symmetry and the continuous rotational symmetry, the excitation spectrum in the angular stripe phase exhibits two gapless Goldstone modes [61], see Fig. 6c. A summary of the properties of these typical phases can be found in Table 1. It should be noted that these phases described above are based on recent experimental configurations with small transferred angular momentum n, and we use them for a brief illustration. It is possible to find more nontrivial phases such as other angular stripe phases with superposition of large-angular-momentum states under the condition of larger n [61, 63] or complex vortex molecule states [62]. Among these typical ground-state phases, the most intriguing one is the angular stripe phase, which attracts intensive research attention and will be discussed in detail in the following.
(Top three panels) Typical spin-component, total density profiles in four distinct phases. (Bottom panel) In a–d, the corresponding angular density-density correlation function \(1-g^{(2)}(\theta )\) is shown. The results for spin-up, spin-down, and total density are indicated by circles, crosses, and solid lines, respectively. Here, I is for the vortex-antivortex pair phase, II is for the half-skyrmion phase, and III and IV are for angular stripe phases. Adapted from Ref. [60]
Table 1 A table of the classification of the typical phases in a realistic SOAM-coupled 87Rb gas with the transferred angular momentum \(n =-1\) at vanishing two-photon detuning \(\delta =0\) [55]
| Vortex-antivortex pair phase | Half-skyrmion phase | Angular stripe phases | Reference | |
|---|---|---|---|---|
| Spin polarizations | \(\langle \sigma _{z}\rangle =0\), \(\langle \sigma _{x}\rangle =-1\) | \(\langle \sigma _{z}\rangle \ne 0\), \(\langle \sigma _{x}\rangle \ne 0\) | \(\langle \sigma _{z}\rangle =0\), \(\langle \sigma _{x}\rangle \ne 0\) | [55, 60, 62] |
| Magnetization | Non-magnetic | Magnetic | Non-magnetic | [55, 60, 62] |
| Coefficients in Eq. (32) | \(\beta =1\) | \(\alpha =1\) or \(\gamma =1\) | \(\alpha =\gamma =1/\sqrt{2}\) or \(\alpha ,\beta ,\gamma \ne 0\) | [60] |
| \(l_z\) in Eq. (30) | 0 | 1 or \(-1\) | Indefinite | [61,62,63] |
| \(\langle \hat{L}_z\rangle\) in \(\psi _{_{l_{z}\uparrow \downarrow }}\) | \((1,-1)\) | (2, 0) or \((0,-2)\) | Indefinite | [61,62,63] |
| Symmetrya | \(\mathcal {T}\) |

| \(\mathcal {T}\) | [62] |
| Symmetry in \(n_{\uparrow \downarrow } (n)\) | \(\mathcal {R} (\mathcal {R})\) | \(\mathcal {R} (\mathcal {R})\) |
\(\mathcal {C}_2 (\mathcal {C}_2)\) or
 \((\mathcal {C}_2)\) \((\mathcal {C}_2)\)
| [60] |
| Single-particle dispersion | Single minimum | Double degeneracy | Double degeneracy | [53, 55, 60, 61] |
| Excitation spectrum | Symmetric, single phonon | Asymmetric, roton structure | Symmetric, two phonons | [60, 61] |
Exotic angular stripe phases
In the past decade, an exotic phase of matter has attracted tremendous attention in ultracold quantum gases, i.e., namely the stripe phase, which breaks spontaneously U(1) gauge symmetry and spatial translational symmetry [56, 97,98,99]. As a consequence, quantum gases will exhibit a superfluid behavior and meanwhile show a periodic modulation in the density distribution. These counterintuitive features associate closely this nontrivial phase to the long-sought supersolid phase in solid Helium since the 1960s [65], i.e., a rigid, spatially ordered solid that flows like a fluid without friction. Whether such a superfluid state can exist remains unclear for more than 50 years until the seminal breakthroughs using ultracold atoms. In 2017, two groups from ETH Zurich and MIT created successfully an ultracold quantum gas featuring supersolid properties using Bose-Einstein condensates with optical cavities or spin-orbit coupling [100, 101]. Later in 2019, three independent groups from Stuttgart, Florence, and Innsbruck observed supersolidity using dipolar quantum gases of lanthanide atoms (i.e., \(^{162}\)Dy, \(^{164}\)Dy, and \(^{166}\)Er) without any external optical lattice [102,103,104], and very recently one of them extended successfully into two dimensions [105].
In the presence of SOAM coupling, several kinds of angular stripe phases are theoretically predicted as introduced above, which take the analogous behavior as that of supersolid. Here, we have discussed two kinds of angular stripe phases: phase (III), a superposition state of two orbital-angular-momentum states (\(l_{z}=\pm 1\)), and phase (IV), a superposition state of three orbital-angular-momentum states (\(l_{z}=0,\pm 1\)). Although experimentalists have achieved successfully most of the ground-state quantum phases of a SOAM-coupled Bose gas, the nontrivial angular stripe phase remains elusive in the laboratory. There are two main obstacles. Firstly, the typical energy scale of the SOAM coupling is about \(E_L\sim 1/R^2\) with the atomic cloud size R. To enhance the SOAM-coupling effect to reach the regime of the angular stripe phase, one needs to reduce the atomic size R which decreases the perimeter of the cloud and instead presents fewer periods of density order in the angular direction. Secondly, recent experimental attempts are made in a \(^{87}\)Rb BEC. The critical Rabi frequency of the angular stripe phase is thus small due to the tiny difference between the intra- and inter-species interactions. As a consequence, the period of stripes becomes so small that the stripes show too low contrast and visibility, which makes them hard to be detected.
The interatomic interaction is one of the crucial factors to affect the parameter space of angular stripe phases as well as the visibility. This is quite similar to the situation when concerning the stripe phase in a SO-coupled Bose gas [56]. The stripe phase prefers the region where the inter-species interaction is pretty smaller than the intra-species interaction. To this end, \(^{41}\)K atomic gases provide a promising candidate for exploring angular stripe phases with tunable interactions according to the Feshbach resonance centered at the magnetic field \(B_{0}=51.95\)G [60]. Near the Feshbach resonance, the intraspecies scattering lengths are approximately constant, and the interspecies one can be tuned in a wide range [106, 107]. By setting typical realistic parameters, the phase diagram is determined and the angular stripe phases can occupy a relatively large parameter space, as shown in Fig. 7. An angular density-density correlation function \(g_{i}^{(2)}(\theta )\equiv \int _{0}^{2\pi }n_{i}(\varphi )n_{i}(\varphi +\theta )\mathrm {d}\varphi /\int _{0}^{2\pi }n_{i}^{2}(\varphi )\mathrm {d}\varphi\) can be introduced to estimate the visibility in density profile, with the angular density \(n_{i}(\varphi )=\int _{0}^{\infty }r\mathrm {d}rn_{i}(r,\varphi )\), and the label \(i=\uparrow ,\downarrow\) for each spin component and null for the total density. In contrast to other phases, the novel angular stripe phases break the rotational symmetry and exhibit spatial density modulation in the angular direction. Two angular stripe phases feature considerable spatial modulation and contrast in the angular density-density correlation for both spin components as well as the total one, as shown in Figs. 5c and d. This hallmark feature might be useful in directly probing the existence of the angular stripes in future experiments with ultracold atoms.
A typical phase diagram in the \(\delta\)-\(\Omega\) plane of a SOAM-coupled \(^{41}\)K gas with inter- and intra-species interactions modulated by the Feshbach resonance technique. The color indicates the expectation value of spin magnetization \(\langle \sigma _z\rangle\) in the condensate wave function determined by a variational approach. The magenta diamonds indicate the regime of angular stripe phase III determined by another imaginary-time propagation method (itpm). The green crosses indicate the selected positions for four distinct phases in Fig. 5, respectively. Here, the Roman numbers stand for the same phases as those in Fig. 5. Adapted from Ref. [60]
There are also other theoretical attempts and developments emphasizing the angular stripe phases in SOAM-coupled Bose gases. For example, by utilizing LG beams with higher-order orbital angular momenta, it is shown that angular stripe phases can be achieved in a wide window of experimentally accessible parameters with high visibility contrast [63, 66]. Besides, A number of distinct quantum phases are identified according to the symmetry analysis, and a complex vortex molecule state is discovered, which plays an important role in the continuous phase transitions [62]. For a ring-shaped BEC in the presence of SOAM coupling, the fine structures of angular stripe phases are explored [64].
SOAM-coupled Fermi gases
The pairing mechanism plays a crucial role in the Fermi superfluid. While it is shown that the SOAM coupling leads to the spin-dependent vortex formation in Bose-Einstein condensates, SOAM coupling alone does not induce vortices in a Fermi superfluid, since fermions in a Cooper pair would acquire opposite orbital angular momenta that cancel each other, yielding a superfluid devoid of vortices. In this section, we are going to discuss the unique features of SOAM-coupled Fermi superfluid at zero temperature, with emphasis on two exotic pairing states, i.e., SOAM-coupling-induced vortex and topological superfluid states.
Pairing physics under SOAM coupling
It is well known that a two-component spin-balance Fermi gas becomes unstable in the presence of an arbitrary small attractive interaction. The resulting instability gives rise to a Bardeen-Cooper-Schrieffer (BCS) ground state with zero center-of-mass momentum. It is also well accepted that in a Fermi superfluid with spin-imbalance or Zeeman fields, exotic pairing states emerge, for instance, Fulde-Ferrell and Larkin-Ovchinnikov states [108, 109], where the former pairing state carries finite center-of-mass momentum and the latter oscillates both in coordinate and momentum spaces, whereas these novel states are only stable in a very small parameter region, which is one of the reasons for the exclusiveness of their experimental observations. However, the experimental achievement of SO coupling in cold atoms offers a new platform to pursue these long sought-after states. For instance, the interplay of SO coupling, Zeeman fields and interactions provides an alternative mechanism to induce Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) states [68,69,70,71,72,73,74]. Besides SO-coupling-induced FFLO states, topological band structures become accessible under SO coupling [39, 40, 110,111,112], which lays the fertile ground for topological superfluid–for instance, aided by the Zeeman fields and interactions, a topological superfluid emerges in a 2D Fermi gas under the Rashba-type SO coupling [113,114,115,116,117,118,119].
Intuitively, SOAM coupling as an angular analog of the conventional SO coupling, two novel pairing states can be expected. One is the SOAM-coupling-induced pairing state with finite quantized angular momenta, which is nothing but a vortex state. The other is the SOAM-coupling-induced angular topological superfluid state, the analog of the topological superfluid state in a one-dimensional lattice gas under a one-dimensional SO coupling, where quantized angular momenta in the former play the role of discretized linear momenta of the latter. In this review, whether the above two expectational pairing states, i.e., SOAM-coupling-induced vortex and topological superfluid states, could be stabilized is clarified. In the following, the former issue will be addressed in Section 5.2 and the latter in Section 5.3.
SOAM-coupling-induced vortex states
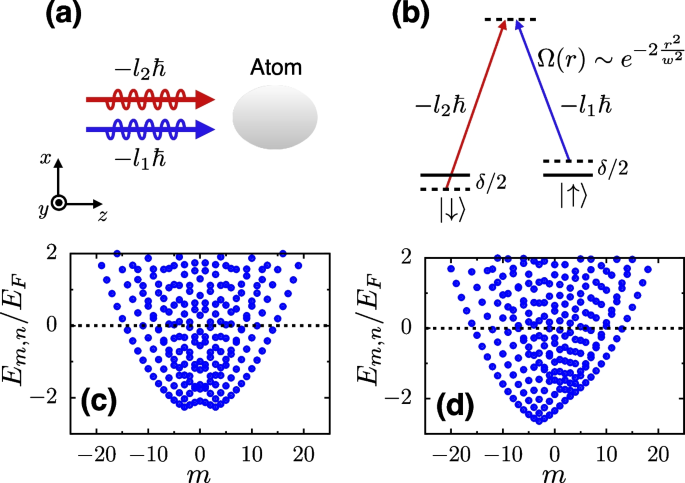
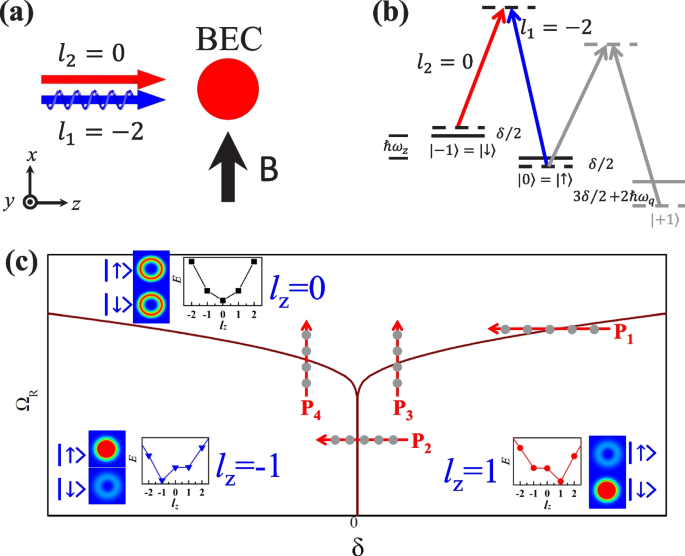
As illustrated in Fig. 8, a two-component Fermi gas is confined in the \(x-y\) plane, where the two ground states are labeled by \(\uparrow\) and \(\downarrow\), respectively. The two-photon Raman process is driven by two copropagating Raman beams carrying different orbital angular momenta \(-l_1\hbar\) and \(-l_2\hbar\) [see Fig. 8a, b] and is characterized by the inhomogeneous Raman coupling \(\Omega (r)\), two-photon detuning \(\delta\), and a phase winding \(e^{-2il\varphi }\). Here, the polar coordinate \(\mathbf {r}=(r,\varphi )\) is taken. After a unitary transformation, the effective single-particle Hamiltonian again reduces to Eq. (17). As we can see that the Raman coupling \(\Omega (r)\) and two-photon detuning \(\delta\) serve as effective transverse and longitudinal Zeeman fields, respectively, which play crucial roles in stabilizing vortices. Different from the LG Raman beams used in previous experiments [53, 55], Chen et al. propose Raman coupling as \(\Omega (r)=\Omega _0 e^{-2r^2/w^2}\) [66], with \(\Omega _0\) the peak intensity and w the beam waist, which can be experimentally realized [120]. Such a choice of the Raman beams is mainly on the basis that the LG Raman beams used in current experiments are suppressed over a considerable region near \(r=0\), giving rise to an almost vanishing spin mixing effect in the vicinity, which is unfavorable for vortex formation essentially. Here, Raman lasers are assumed to operate at the tune-out wavelength [55, 83, 84], leading to a vanishing diagonal ac-stark potential that is consistent with the experiment [55]. The external potential \(V_{ext}(r)\) is chosen as an isotropic hard-wall box trap with a radius R, which offers a natural boundary.
a SOAM coupling in atoms induced by a pair of copropagating Raman beams carrying different orbital angular momenta (\(-l_1\hbar\) and \(-l_2\hbar\)), with a transferred angular momentum \(2l\hbar =(l_1-l_2)\hbar\). b Schematic illustration of the level scheme. c, d Single-particle energy spectra under SOAM coupling for \(\delta =0\) (c), and \(\delta /E_F= 0.4\) (d) with \(E_F=\hbar ^2 k^2_F/(2M)\) the Fermi energy and \(k_F\) the Fermi vector. Black dashed lines denote potential Fermi surfaces in a many-body setting. Adapted from Ref. [66]
It is helpful for understanding the mechanism of vortex formation by analysis of the single-particle properties before moving to the many-body calculation. Figure 8c and d illustrate the impact of the two-photon detuning \(\delta\) on the single-particle spectrum. At the resonance with \(\delta =0\), the time-reversal symmetry gives rise to \(E_{m,n}=E_{-m,n}\), whereas away from the resonance at finite \(\delta\), the breaking of the time-reversal symmetry results in a deformation of the Fermi surface. In the many-body setting when the attractive interaction is taken into account, pairing predominantly occurs between unlike spins with the same radial quantum number n to maximize the overlap of radial wave functions. Thus, for the symmetric eigenspectrum under \(\delta =0\), it is more favorable for two fermions with opposite angular quantum numbers (m and \(-m\)), forming a Cooper pair with a zero total angular momenta. In contrast, under a finite \(\delta\) with asymmetric eigenspectrum, the two fermions in a Cooper pair may possess different values of |m|, leading to a pairing state with a nonzero quantized angular momentum, which is the so-called vortex state. Such a mechanism for the vortex formation is analogous to that of the SO-coupling-induced Fulde-Ferrell states, where the interplay between SO coupling and Zeeman fields gives rise to the deformation of Fermi surfaces with broken time-reversal symmetry in the momentum space [70,71,72,73,74].
Chen et al. confirm the above analysis by solving the many-body problem under the Bogoliubov–de Gennes (BdG) formalism [66]. Specifically, the order parameter is written in the form of \(\Delta (\mathbf {r})=\Delta (r)e^{i \kappa \varphi }\), where the vorticity \(\kappa =0\) (\(\kappa \ne 0\)) indicates the superfluid (vortex) state. With different \(\kappa \in \mathbb {Z}\), the BdG equation and \(\Delta (\mathbf {r})\) are solved self-consistently with a fixed particle number. The ground state is then determined by comparing the free energies of vortex states with different \(\kappa\), the usual superfluid state (\(\kappa =0\)), and the normal state (\(\Delta =0\)).
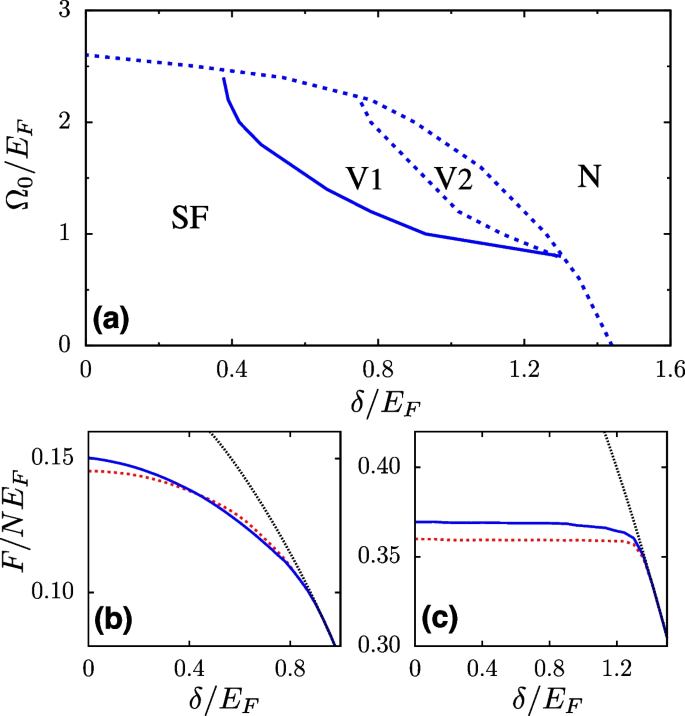
As shown in Fig. 9a, Chen et al. give a typical phase diagram of the system with SOAM coupling in the \(\Omega _0\)–\(\delta\) plane. For \(\delta >0\) (\(\delta <0\)), vortex states with \(\kappa =-1\) (\(\kappa =1\)) emerge, with the phase boundaries unchanged to the sign of \(\delta\). At small \(\Omega _0\) and \(\delta\), the ground state is a usual superfluid (SF) with a zero vorticity \(\kappa =0\). Under sufficiently large \(\Omega _0\) and/or \(\delta\), the free-energy difference between the SF and normal (N) states becomes vanishingly small and hence the system enters the normal state. Remarkably, two vortex states emerge between SF and N states. For example, with a fixed \(\Omega _0/E_F=1.5\) [see Fig. 9a], the ground state is in the SF state under small detunings \(\delta\), and becomes a fully gapped vortex state (V1) beyond a critical value of \(\delta\). Further increase of \(\delta\) gives rise to a gapless vortex state (V2), whose bulk excitation gap closes. In Figs. 9b, c, free energies of different states are compared, as the phase diagram is traversed. Especially, for the case with \(\Omega _0=0.5E_F\), the ground state remains vortexless for finite \(\delta\), despite the deformation of the Fermi surface under SOAM coupling and effective Zeeman fields. This originates from the quantized nature of the angular momentum, and is on the sharp contrary to the SO-coupling-induced Fulde-Ferrell state which carries a nonzero, continuously varying center-of-mass momentum in the presence of SO coupling and Zeeman fields [68,69,70,71,72,73,74].
a Phase diagram of a two-dimensional Fermi superfluid with SOAM coupling in the \(\Omega _0\)-\(\delta\) plane. The phase diagram includes the usual superfluid state with \(\kappa =0\), the normal state with \(\Delta =0\), and two vortex states with \(\kappa =-1\): a fully gapped vortex states (V1) and a gapless vortex state (V2). b, c Free energies F of the superfluid (\(\kappa =0\); red dashed), vortex (\(\kappa =-1\); blue solid), and normal (black dotted) states as functions of \(\delta\), with \(\Omega _0/E_F=2\) (b) and \(\Omega _0/E_F=0.5\) (c). Adapted from Ref. [66]
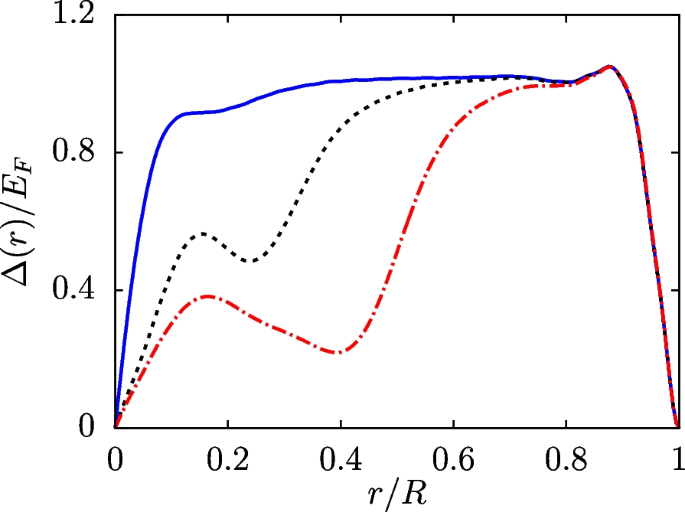
Remarkably, as illustrated in Fig. 10, the SOAM-induced vortex state features a giant and tunable vortex-core size, similar to that in a BEC interacting with a microwave field [121]. The vortex-core size, characterized by variations of the order parameter, is comparable to the waist w of LG beams. Compared to the conventional vortex states in atomic Fermi superfluids, where changes in the vortex-core structure predominantly take place within a short length scale set by the interatomic separation [75, 76], these SOAM-coupling-induced vortex states, with tunable size and core structure, provide unprecedented experimental access to topological defects in Fermi superfluids.
Order parameter profiles for \(k_Fw=5\) (blue solid), \(k_Fw=10\) (black dashed), and \(k_Fw=15\) (red dash-dotted). We fix \(\delta /E_F=0.84\) and \(k_FR=15\). Adapted from Ref. [66]
Different from Chen et al.’s configuration, Wang et al. investigate a similar vortex-forming scheme under SOAM coupling [67]. Most strikingly, they predict that an unprecedented vortex state, which is an angular analog of SO-coupling-induced Larkin-Ovchinnikov state, to occur.
Nevertheless, for the inevitable heating introduced by the Raman process, it is difficult to cool a realistic Fermi gas with SOAM coupling below the superfluid temperature [122], which leads to the exclusiveness of SOAM-coupling-induced novel states. Instead, concerning the persistence of dressed molecules above the critical temperature in Fermi gases with SO coupling [19, 79], it is reasonable to expect that molecular states in a SOAM-coupled Fermi gas should be readily accessible under typical experimental conditions. Based on the above consideration, Han et al. studied the two-body bound states in a SOAM-coupled quantum gas of fermions very recently [80]. They identify the condition for the emergence of molecular states with finite total angular momenta and propose to detect the molecules according to the radio-frequency spectroscopy. As the molecular states can form above the superfluid transition temperature, Han et al. offer an experimentally more accessible route toward the study of the underlying pairing mechanism under SOAM coupling.
SOAM-coupling-induced topological states
As discussed in Section 5.1, it is expected that SOAM coupling can induce a topological superfluid with the help of Zeeman fields and interactions, while implementation of SOAM coupling relies on the spatial dependence of the LG beams, which gives rise to the dimensionality of atomic gases must higher than one, whereas it is also realized that the Fermi superfluid becomes gapless and losses its topological features when its spatial dimensionality higher than that of SO coupling [70, 123], such that the one-dimensional nature of the SOAM coupling (coupling only occurs along the azimuthal direction) imposes a stringent constraint on the stability of an angular topological superfluid. Whether such a topological superfluid can also be stabilized under SOAM coupling should be verified. It is shown that the stability of a fully gapped angular topological superfluid survives the constraint above, provided that the radial motion of atoms is sufficiently suppressed and then the topological gap is not closed [78].
The survival of the angular topological superfluid can be understood through the following analysis. As shown in Eq. (17), the Raman coupling and the diagonal ac-stark potential can be written as \(\Omega (r)=\Omega _0 I(r)\) and \(\chi (r)=\chi _0 I(r)\), consistent with configurations of current experiments on SOAM coupling [53, 55]. Here, \(\Omega _0\) is the effective SOAM-coupling strength, \(\chi _0\) is the trapping strength of the diagonal ac-stark potential, and \(I(r)= (\sqrt{2}r/w)^{2l}e^{-2 r^2 /w^2}\) is the spatial intensity profile of LG lasers, with w the beam waist. Different from the SOAM-induced vortex state in Section 5.2, here, \(\chi (r)\) provides an extra confinement potential, which plays an important role in stabilizing the topological superfluid. For a confinement that is sufficiently tight along the radial direction, the radial degrees of freedom of the atoms are frozen, and the remaining quantized angular motion is then well-captured by an effective one-dimensional model with discretized modes. Intuitively, such a scenario occurs when the trap depth \(\chi _0\) is so large that the radial excitation energy (\(\sim \sqrt{ |\chi _0| \hbar ^2 /(m w^2)}\)) becomes much larger than any other relevant energy scales of the system. The atoms are then localized near \(r_0=\sqrt{l/2}w\) in the radial direction and the system reduces to an effective one-dimensional model along the angular direction.
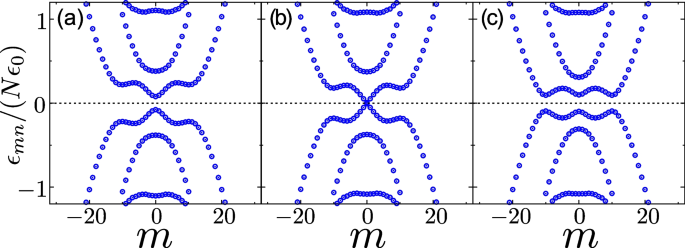
The above analysis is confirmed through the BdG approach [78]. As illustrated in Fig. 11, Chen et al. show the Bogoliubov quasiparticle spectrum in a sufficiently deep ac-stark potential with \(\chi _0/\epsilon _0=-8\) in the unit of energy \(\epsilon _0=\pi ^2 \hbar ^2/(2M r^2_0)\). For the case with \(\delta =0\), the ground state always emerges at \(\kappa =0\). Here, consistent with Section 5.2, the vorticity \(\kappa =0\) (\(\kappa \ne 0\)) denotes the superfluid (vortex) state. By increasing the coupling strength \(\Omega _0\), the Bogoliubov spectrum undergoes a gap-closing and re-opening process, reminiscent of that of a topological phase transition. Specifically, the Bogoliubov quasiparticle excitation is fully gapped under small \(\Omega _0\) [Fig. 11a], and then becomes gapless at a critical \(\Omega ^{c}_0/\epsilon _0\approx 0.18\) [Fig. 11b], and finally is again fully gapped for further increasing \(\Omega _0\) [Fig. 11(c)]. The process of gap closing and re-opening is further demonstrated as a topological phase transition by calculating the Zak phase of the one-dimensional effective Hamiltonian [78]. Besides, it is also demonstrated that the angular topological superfluid is stabilized when the ac-stark potential becomes sufficiently large.
Bogoliubov spectra of the Fermi superfluid under SOAM coupling, with a vanishing two-photon detuning \(\delta =0\), and an increasing \(\Omega _0\): a \(\Omega _0/\epsilon _0=0.15\), b \(\Omega _0/\epsilon _0=0.18\), and c \(\Omega _0/\epsilon _0=0.2\). Adapted from Ref. [78]
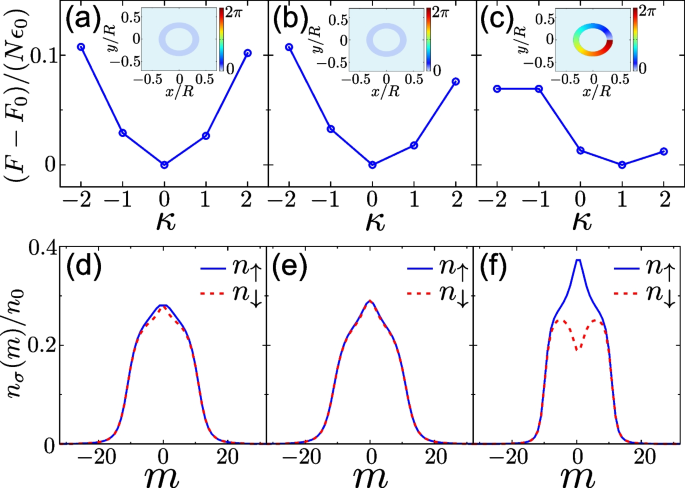
Building upon the topological superfluid state above, an exotic topological vortex state can be induced by taking the two-photon detuning \(\delta\) into account, which deforms the Fermi surface. As shown in Fig. 12a–c, the free energy is generically asymmetric with respect to \(\kappa =0\) at a finite \(\delta\). The asymmetry becomes more apparent with increasing \(\Omega _0\), until the ground-state order parameter eventually acquires a finite phase with \(\kappa \ne 0\). Intriguingly, such a transition into the vortex state is topological. As demonstrated in [78], while the Fermi-surface deformation is manifested as the asymmetric spectral shape with respect to \(m=0\), the closing and re-opening of the energy gap persist. Indeed, after the gap is reopened, the angular momentum of the ground state jumps from \(\kappa =0\) to \(\kappa =1\). The ground state simultaneously becomes topological, which is confirmed by the Zak-phase calculation. Conceptually, such an exotic topological vortex state is the angular version of the topological Fulde-Ferrell state under the conventional SO coupling [71,72,73,74].
a–c Free energies of pairing states as functions of \(\kappa\), with a fixed two-photon detuning \(\delta /\epsilon _0=-1.6\). The insets show the phase of the order parameter. Here, \(F_0\) denotes the ground-state free energy. d–f Density distribution of the ground state in the angular-momentum space, where we define \(n_0=N/(\pi r^2_0)\). Here, the blue solid (red dashed) curve denotes the density distribution of spin-up (spin-down) component. a, d and b, e are the vortexless superfluid states with \(\Omega _0/\epsilon _0=0.1\) and 0.16, respectively. c, f is a topological vortex state with \(\Omega _0/\epsilon _0=0.18\). Adapted from Ref. [78]
In addition, the topological vortex leaves a direct signature in the angular-momentum-space density profile, as illustrated in Fig. 12d–f. The density profile of the minority spin species exhibits a dip close to \(\kappa /2\) only in the topological vortex state [Fig. 12f], since the spin polarization in the vortex state is a direct result of the two-photon detuning, which plays the role of an effective Zeeman field. Similar signatures have been identified in the topological Fulde-Ferrell state under SO coupling.
The origin of angular topological superfluid comes from the interplay of interactions, Zeeman fields, and SOAM couplings. As topological superfluids are believed to host Majorana zero modes at boundaries, once a boundary is created, for instance, by shining a strong laser beam to break the ring geometry of the ac stark potential, Majorana zero modes should be observed.
Experiment achievements
The SOAM coupling has been achieved in \(^{87}\)Rb Bose gases independently by two experiment groups [53,54,55], following the earlier theoretical proposals [46,47,48]. The Zeeman sublevels of the ground hyperfine manifold |F = 1\(\rangle\) are coupled by a pair of copropagating LG beams according to a Raman transition. It leads to an orbital angular momentum change of atoms during the transition between the ground Zeeman states, which play the role of spin. The realization of SOAM coupling in cold atoms has recently been reported in a spin-1 \(^{87}\)Rb BEC [53], in which the atoms are loaded into the middle-energy state of three Raman-dressed states. The correlations between spin and orbital angular momentum in this Raman-dressed state are confirmed. Then, the ground-state quantum phase transitions are observed in the same bosonic system [54], known as the Hess-Fairbank effect [124, 125]. Meanwhile, the SOAM coupling was also demonstrated in an effective spin-half atomic gas [55], following a similar Raman scheme. The ground-state phase diagram is comprehensively studied, and the first-order phase transitions are identified. In the follows, we are going to introduce the main achievements in these experiments.
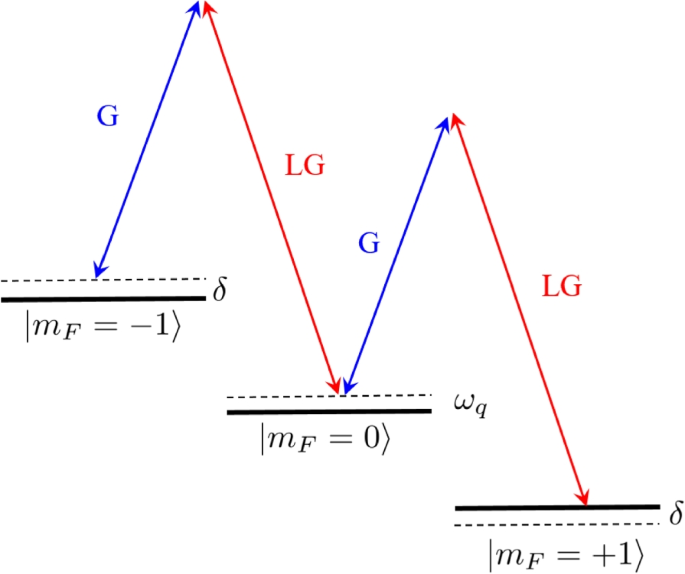
In the experiment of Lin’s group [53], the three hyperfine states of the ground-state manifold \(\left| F=1,m_{F}=0,\pm 1\right\rangle\) of \(^{87}\)Rb atoms are coupled by a pair of Raman beams as illustrated in Fig. 13, one of which is an LG beam carrying orbital angular momentum \(l=1\). The center-of-mass angular momentum of atoms changes during the transition between different hyperfine states. This effectively produces a light-induced effect of a spin \(\left| \mathbf {F}\right| =1\) particle moving in a magnetic Zeeman field \(\symbf{\Omega }_{eff}\), which results in a SOAM coupling after a local spin rotation. In the experiment, the BEC is initially prepared in the bare hyperfine state \(\left| m_{F}=-1\right\rangle\), and then is transferred to \(\left| m_{F}=0\right\rangle\). After slowly switching on the Raman fields, the atoms are adiabatically loaded into the Raman-dressed polar state \(\left| \xi _{0}\right\rangle\) with \(\left\langle \mathbf {F}\right\rangle =0\), the middle-energy eigenstate of \(\symbf{\Omega }_{eff}\cdot \mathbf {F}\) with the form of [126]
in the bare hyperfine basis \(\left| m_{F}=0,\pm 1\right\rangle\), where \(\beta \left( r\right) =\arctan \left[ \Omega \left( r\right) /\delta \right]\) is the polar angle of the light-induced magnetic Zeeman field \(\symbf{\Omega }_{eff}\). Here, \(\Omega \left( r\right)\) is the Raman-coupling strength and \(\delta\) is the Raman detuning. After the adiabatic loading, one easily finds a correlation between the atom spin (hyperfine state) and its orbital angular momentum: the atoms acquire an orbital angular momentum \(\Delta l=1\) (\(\Delta l=-1\)) when transitioning from \(\left| m_{F}=0\right\rangle\) to \(\left| m_{F}=-1\right\rangle\) (\(\left| m_{F}=+1\right\rangle\)). Therefore, the vortex structures are anticipated in the bare hyperfine states \(\left| m_{F}=\pm 1\right\rangle\). The Raman-dressed state \(\left| \xi _{0}\right\rangle\) is conveniently characterized by the QAM \(l_{z}=0\) in the rotating frame, and the angular momenta of bare hyperfine states in the laboratory frame are, respectively, \(l_{m_{F}=0}=l_{z}\) and \(l_{m_{F}=\pm 1}=l_{z}\mp 1\).
The schematic of energy-level diagram of Raman transition in [53]. The hyperfine states of the ground-state manifold \(\left| F=1\right\rangle\) of \(^{87}\)Rb atoms are coupled by a pair of Raman beams, in which one is a LG beam denoted by “LG” and the other one is a Gaussian beam denoted by “G.” Here, \(\delta\) is the Raman detuning that is tunable in the experiment, and \(\omega _{q}\approx 2\pi \times 50\)Hz is the quadratic Zeeman shift
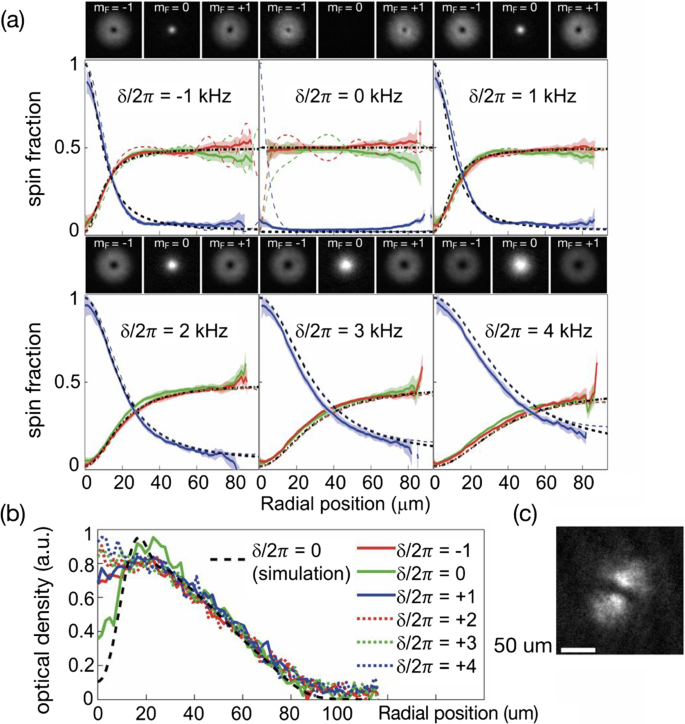
The vortex structures in the bare hyperfine states could be probed according to a Stern-Gerlach scheme after a time-of-flight (TOF) expansion by simultaneously turning off the Raman beams and external trap. The density profile of bare hyperfine components \(\left| m_{F}\right\rangle\) after 24 ms TOF with holding time 1 ms are presented in Fig. 14a for different Raman detunings, as well as the corresponding total density profile (or optical density) presented in Fig. 14b. It is easily found that the \(\left| m_{F}=0\right\rangle\) component carries zero angular momentum, while the \(\left| m_{F}=\pm 1\right\rangle\) components carry the same magnitude of angular momentum indicated from their same hole sizes. The interference pattern between \(\left| m_{F}=\pm 1\right\rangle\) components shown in Fig. 14c implies that they carry the opposite rotation directions of vortices with angular momentum \(l=\mp 1\).
Demonstration of SOAM coupling in \(^{87}\)Rb BEC adiabatically loaded into the Raman-dressed state \(\left| \xi _{0}\right\rangle\). The images are taken after 24 ms TOF with holding time 1 ms. a The density profiles of bare hyperfine components \(\left| m_{F}\right\rangle\) for different Raman detunings. The blue, red, and green curves are experimental data for \(\left| 0\right\rangle\), \(\left| +1\right\rangle\), and \(\left| -1\right\rangle\) components, respectively. The black dashed (dash-dotted) curve denotes the predictions from Eq. (33) magnified by 9.1 in the radial position for \(\left| 0\right\rangle\) (\(\left| \pm 1\right\rangle\)), while the colored dashed curves are the full numerical simulations of TOF from 3D time-dependent Schördinger equation. b Radial cross section of the total optical density. Colored solid and dotted (black dashed) curves indicate the experimental data (TOF simulation at \(\delta =0\)). c Interference pattern between \(\left| \pm 1\right\rangle\) components at \(\delta =0\). Adapted from Ref. [53]
While the SOAM coupling is demonstrated according to adiabatically loading atoms into the middle-energy Raman-dressed state \(\left| \xi _{0}\right\rangle\), the effective light-induced gauge potential in this dressed state is zero, i.e., \(\mathbf {A}_{0}=0\) [53], which leads to a vanishing magnetic field experienced by atoms, i.e., \(\mathbf {B}=\nabla \times \mathbf {A}_{0}\). Subsequently, Lin’s group further reports the realization of non-zero gauge potential with SOAM coupling by adiabatically loading atoms into the Raman-dressed state \(\left| \xi _{-1}\right\rangle\), the lowest-energy eigenstate of \(\symbf{\Omega }_{eff}\cdot \mathbf {F}\) [54, 126],
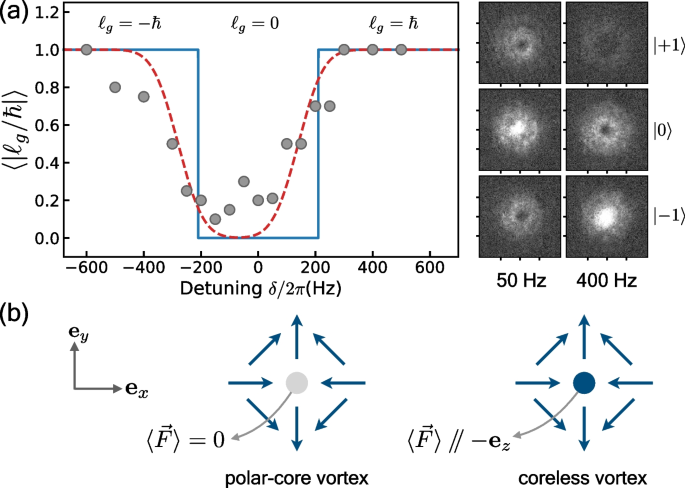
where \(\theta +\gamma\) is the phase introduced by a gauge transformation. Then, an azimuthal gauge potential is induced by SOAM coupling, taking the form of \(A_{-1}=\left( \hbar /r\right) \cos \beta\) under the choice of \(\theta +\gamma =0\), which gives rise to an effective magnetic field experienced by atoms. The magnetic flux through the atomic cloud can be tuned via the Raman detuning \(\delta\). This leads to a phase transition of the SOAM-coupled ground state from one to another QAM. In the experiment [54], it is demonstrated that the QAM of the ground state changes from \(l_{g}=\pm 1\) to 0 as the Raman detuning \(\left| \delta \right|\) continuously decreases. The phase transition occurs at the critical Raman detuning \(\left| \delta \right| \approx 2\pi \times 210\)Hz as shown in Fig. 15a. At a detuning below the critical value, i.e., \(\delta =2\pi \times 50\)Hz, the system stays at the ground state with QAM \(l_{g}=0\). The corresponding mechanical angular momenta of bare hyperfine states \(\left| m_{F}\right\rangle\) are \(l_{m_{F}}=\left( 1,0,-1\right)\) for \(m_{F}=\left( +1,0,-1\right)\) in the laboratory frame. The same hole sizes in the \(\left| m_{F}=+1\right\rangle\) and \(\left| m_{F}=-1\right\rangle\) are observed in the experiment as shown in Fig. 15a. At a detuning above the critical value, i.e., \(\delta =2\pi \times 400\)Hz, the SOAM-coupled ground state transits to the state with QAM \(l_{g}=1\), which corresponds to the mechanical angular momenta of bare hyperfine states \(l_{m_{F}}=\left( 2,1,0\right)\) for \(m_{F}=+1,0,-1\) in the laboratory frame. Then the vortex with larger hole size in \(\left| m_{F}=+1\right\rangle\), compared to that in \(\left| m_{F}=-1\right\rangle\), is anticipated and is experimentally confirmed.
a Observation of the phase transition of the SOAM-coupled ground state between \(\left| l_{g}\right| =1\) and \(l_{g}=0\) states. The solid and dashed lines are the calculations for the ideal case and that including the detuning noise in the experiment. Then, density profiles of bare hyperfine states at \(\delta /2\pi =50\) and 400Hz are displayed, corresponding to the QAMs \(l_{g}=0\) and 1, respectively. b Schematic of the spin textures at \(\delta >0\), where the arrows show the direction of the transverse spin \(\left( \left\langle F_{x}\right\rangle ,\left\langle F_{y}\right\rangle \right)\). Adapted from Ref. [54]
Soon, the ground-state quantum phase diagram of this SOAM-coupled system is comprehensively studied in an effective spin-half \(^{87}\)Rb atomic gas [55]. Due to a larger quadratic Zeeman shift \(\omega _{q}=2\pi \times 5.52\)kHz compared to that of [53, 54], the third Zeeman hyperfine state \(\left| F=1,m_{F}=+1\right\rangle\) is far-off-resonant, and is then dropped out from the problem. In addition, one of the two Raman beams is operated in a higher LG mode with a winding number \(l_{1}=-2\). It gives rise to a rich ground-state phase diagram as presented in Fig. 16. The whole system is therefore governed by the Hamiltonian (15) in the presence of LG Raman beams, which introduces an effective SOAM coupling \(\hat{L}_{z}\hat{\sigma }_{z}\) as seen in Eq. (17) after a unitary transformation. Here, a tune-out wavelength of LG beams is chosen [127]. It ensures that any observed circular structure of atomic clouds is resulted from the vortex formation due to the SOAM coupling, excluding the trapping effect of the diagonal ac-stark potential \(\chi \left( r\right)\) of LG beams.
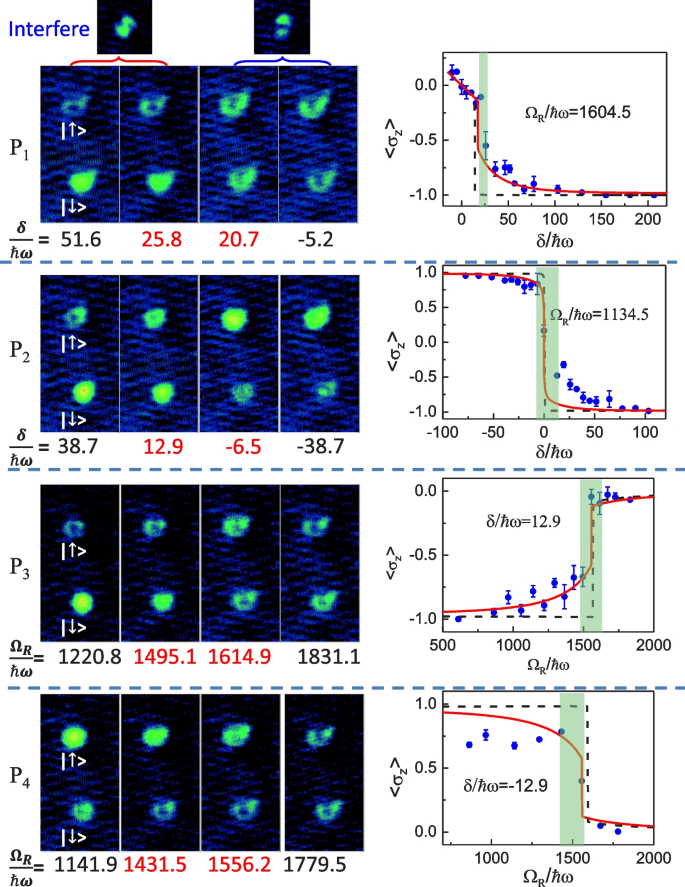
Schematic of SOAM coupling. a Experimental setup. b The energy diagram of Raman transition. The hyperfine states \(\left| m_{F}=0\right\rangle =\left| \uparrow \right\rangle\) and \(\left| m_{F}=-1\right\rangle =\left| \downarrow \right\rangle\) are coupled by a pair of Raman beams, one of which is operated in the LG mode with a winding number \(l_{1}=-2\). The third hyperfine state \(\left| m_{F}=+1\right\rangle\) is far-off-resonant due to a large quadratic Zeeman shift \(\omega _{q}\approx 2\pi \times 5.52\)kHz. Here, \(\delta\) is the two-photon detuning. c The ground-state phase diagram. Three single-particle ground-state phases are characterized by the QAM \(l_{z}=0,\pm 1\). The corresponding lowest-band dispersion as well as the typical density profiles is illustrated in the insets. Here, the phase transitions are studied in the experiment following four typical paths \(P_{1,2,3,4}\). Adapted From Ref. [55]
In order to explore the ground-state quantum phases of the system, the Raman beams need to be introduced adiabatically. After preparing the BEC in the hyperfine state \(\left| m_{F}=-1\right\rangle\) by setting a large detuning \(\delta =2\pi \times 400\)kHz, the Raman beams are turned on. Then, the detuning \(\delta\) is ramped to the desired value adiabatically. This process keeps the system remaining in the ground state all the time. Subsequently, the transitions between different ground-state quantum phases could be studied following different paths \(P_{1,2,3,4}\) as shown in Fig. 16c. For example, along the path \(P_{1}\), the Raman coupling strength is fixed at \(\Omega _{R}/\hbar \omega =1604.5\) in the unit of harmonic energy, while the detuning \(\delta\) adiabatically decreases across the phase boundary. The SOAM-coupled system transits from the half-skyrmion phase with QAM \(l_{z}=1\) to the vortex-antivortex phase with QAM \(l_{z}=0\). The phase transition can experimentally be identified according to the change of density profiles of bare hyperfine states: the vortex structure exists only in the spin-\(\uparrow\) atomic cloud in the half-skyrmion phase, while both spin states exhibit vortex formations in the vortex-antivortex phase. The analogous procedures are performed along the paths \(P_{2,3,4}\).
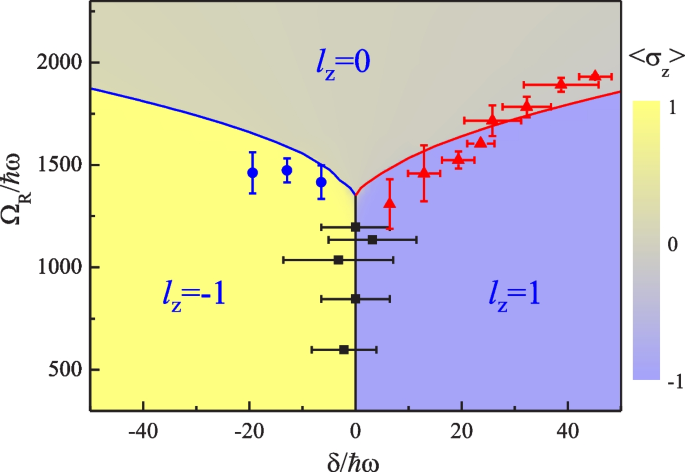
The spin-resolved density profiles are presented in Fig. 17 across different phase boundaries. To confirm the formation of vortices that the circular structures of atom clouds carry angular momenta, a resonant radio-frequency (rf) pulse is applied that transfers the atoms between internal Zeeman hyperfine states \(\left| \uparrow \right\rangle\) and \(\left| \downarrow \right\rangle\) [128,129,130]. The appearance of the interference pattern in each spin component during TOF, as shown in Fig. 17, implies that the circular structures are indeed vortices before the rf transition. The spin polarization \(\left\langle \hat{\sigma }_{z}\right\rangle =\left( N_{\uparrow }-N_{\downarrow }\right) /\left( N_{\uparrow }+N_{\downarrow }\right)\) is an additional indicator of the phase transitions, which jumps among \(\left\langle \hat{\sigma }_{z}\right\rangle =0,\pm 1\) across different phase boundaries. Here, \(N_{\uparrow \left( \downarrow \right) }\) is the atom number for the spin-\(\uparrow \left( \downarrow \right)\)component. The spin polarization is presented as a function of the two-photon detuning \(\delta\) in Fig. 17. The evident jump behavior during phase transitions is observed in the experiment even at finite temperatures. Regarding these characteristic behaviors across the phase transitions, it allows us to identify the boundaries of different ground-state quantum phases. Then the ground-state phase diagram is conveniently mapped out in the parameter space spanned by the detuning \(\delta\) and the coupling strength \(\Omega _{R}\), as illustrated in Fig. 18.
The spin-resolved density profiles after a 20 ms TOF expansion across different phase-transition boundaries along four exemplary paths \(P_{1,2,3,4}\) (left panel) and the corresponding spin polarization \(\left\langle \hat{\sigma }_{z}\right\rangle\) (right panel). The black dashed (red solid) curve is the theoretical prediction at zero temperature (at finite temperature \(T/T_{c}=0.32\)). Adapted from Ref. [55]
The ground-state phase diagram of a SOAM-coupled condensate. Three quantum phases are characterized by QAMs \(l_{z}=0,\pm 1\). The solid curves denote the phase boundaries predicted by the mean-field theory, which are experimentally confirmed. The background color denotes the spin polarization \(\left\langle \hat{\sigma }_{z}\right\rangle\). Adapted from Ref. [55]
Conclusions and outlooks
In conclusion, the most recent advances in both the theories and experiments of spin-orbital-angular-momentum (SOAM) coupled quantum gases are briefly summarized in this review. The basic idea of engineering SOAM coupling in ultracold atoms is presented, and exotic quantum phases of Bose gases are introduced as well as those of Fermi gases in the presence of SOAM coupling. In spite of remarkable progress in this field, it is far from the end of the story. There could be further developments in SOAM-coupled quantum gases, since several issues still require more theoretical and experimental efforts.
Few-body physics—As a building block of interacting many-body systems, the few-body problem is of important significance in ultracold atoms. For instance, the two-body physics determines the essential interaction parameter in the many-body Hamiltonian and even dominates crucial quantum correlations in many-body systems, such as Tan’s relations [131,132,133]. Besides, the few-body problem itself displays intriguing features such as the Feshbach resonance and Efimov effect. The few-body problem has intensively been studied in spin-linear-momentum-coupled quantum gases [134,135,136,137,138,139,140], while the theory for SOAM-coupled systems is still elusive to date. Rich physics in this new few-body system is remained to be discovered in near future, which could provide deep insight into many-body properties of SOAM-coupled quantum gases.
Finite-temperature phase diagrams—The current theory of SOAM-coupled quantum systems is constructed in the framework of the zero-temperature mean-field theory. For example, the ground-state quantum phases of Bose gases are based on the solution of the Gross-Pitaevskii equation, while the giant vortex Fermi superfluid is predicted by the zero-temperature Bogoliubov-de Gennes formalism. The natural question arises whether these exotic quantum phases are stable enough against the thermal fluctuation at finite temperature as well as against the quantum fluctuation at zero temperature beyond the mean-field theory [58]. A more comprehensive theoretical analysis is required to address these issues and is necessary for the comparison with experimental observations as well.
Experimental perspectives—The angular stripe phases of SOAM-coupled Bose gases have not yet been observed in experiments. It is energetically favored for an intraspecies interaction strength larger than the interspecies one (i.e., \(g_{\uparrow \uparrow },g_{\downarrow \downarrow }>g_{\uparrow \downarrow }\)). However, there is no convenient Feshbach resonance of \(^{87}\)Rb atoms to adjust interactions. The angular stripe phase lies in a narrow parameter window due to the small difference between \(g_{\uparrow \uparrow }\) (or \(g_{\downarrow \downarrow }\)) and \(g_{\uparrow \downarrow }\) for \(^{87}\)Rb atomic gases. For this reason, the \(^{41}\)K atomic gas becomes one of the promising candidates for future experiments [60], in which the interspecies scattering length can be tuned in a wide range near the Feshbach resonance centered at the magnetic field \(B_{0}=51.95\)G, while the intraspecies scattering lengths are approximately constant. By choosing appropriately the interatomic scattering lengths, the window of angular stripe phases in the parameter space is enlarged, which can be operated easily in experiments [60].
Moreover, the SOAM coupling is not realized in Fermi gases at present, which would provide a new platform to investigate exotic vortex and topological superfluid states. Other interesting directions, such as the non-equilibrium or the dynamics, BCS-BEC crossover, and quantum fluctuations of Fermi gases with SOAM coupling are yet to be explored. All these fascinating and remarkable phenomena are devoted to future studies.