One among the fields advanced by quantum mechanics is metrology, which concerns the estimation of unknown physical parameters [1,2,3,4,5] aiming at improving the estimation beyond classical precision bounds. Higher estimation precision demands more resources. The trade-off between the precision and the resources is constrained by the quantum Cramér-Rao bound (QCRB), which states that the variance of the estimation is at least as high as the inverse of the quantum Fisher information [6,7,8,9,10,11,12,13]. To attain the highest achievable precision, one needs to optimize over the input state and the encoding Hamiltonian as well as the measurements performed at the output.

In the past decades since Yuen and Lax [14] who first proposed an idea to estimate a complex parameter by measuring non-Hermitian observables, no progress has been made in the improvement of parameter estimation by optimizations of measurements invoking non-Hermitian operators. The reason is probably that in quantum mechanics observables are represented by Hermitian operators. In the last two decades, the study of non-Hermitian system and their unique properties have attracted fast growing interest [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29], this motivates the examination of parameter estimation involving non-Hermitian operators. We should address that there are estimation protocols (or sensors) based on non-Hermitian system recently [30,31,32,33,34,35,36,37,38], but all analyses so far are based on either the quantum Fisher information and quantum Cramér-Rao bound with Hermitian operators or the properties of exceptional points. There is no study of quantum Cramér-Rao bound and its consequent estimation theory based on measurements of non-Hermitian operators.

In this paper, inspiring by the recent progress on the measurement of non-Hermitian operators [39,40,41,42,43], we present a scheme to enhance the precision of parameter estimation by measurement of non-Hermitian operators. To this goal, we first derive a previously unknown quantum Cramér-Rao bound defined by a quantum Fisher information for non-Hermitian operators. We find that the Fisher information is significantly increased due to the optimization over measurements including non-Hermitian operators, in particular for systems in mixed states. This is in contrary to the results of the quantum Fisher information defined by symmetric logarithmic derivatives. Saturation of the bound is analyzed and the optimal measurement to attain the bounds is derived. We demonstrate the present theory with the phase estimation setup in trapped ions [5, 44] and the adiabatic quantum parameter estimation setup.

The remainder of this paper is organized as follows. In Section 2, we first give the Robertson-Schrödinger uncertainty relation for non-Hermitian operators and extend the error propagation function from Hermitian systems [45, 46] to non-Hermitian systems. Then, we present a bound for parameter estimation based on the quantum Fisher information invoking measurements of non-Hermitian operators. An expression for the quantum Fisher information is derived and the optimal measurement to saturate the bound is given. In Section 3, we apply this theory to quantum parameter estimation with GHZ states of ions and show that mixed states can further enhance the sensitivity of phase estimation with measurements of non-Hermitian operators. The optimal measurement for this setup is derived in details. In Section 4, we apply this theory to adiabatic quantum parameter estimation, taking the estimation of magnetic field on a nuclear magnetic resonance as an example. The measurement of the non-Hermitian optimal operator is discussed in Section 5, and finally we conclude in Section 6.

In this section, we first give the Robertson-Schrödinger uncertainty relation for non-Hermitian operators. Then, the error propagation is extended from Hermitian to non-Hermitian systems. Finally, we derive the non-Hermitian quantum Fisher information based on the new error propagation.

2.1 Robertson-Schrödinger uncertainty relation for non-Hermitian operators

In order to present a Robertson-Schrödinger uncertainty relation for non-Hermitian operators that will be used to derive a non-Hermitian quantum Fisher information with non-Hermitian operators, let us consider two linear operators A and B, which can be either Hermitian or non-Hermitian. Defining \(\Delta A=A-\langle A\rangle\), \(\Delta B=B-\langle B\rangle\) and

as the variance for operator \(O\,\) (\(O=A,B\)), the Robertson-Schrödinger uncertainty relation follows from the Schwarz inequality \(\langle F\vert F\rangle \langle G\vert G\rangle \ge \vert \langle F\vert G\rangle \vert ^2\) with \(\vert F\rangle =\Delta A\vert \Psi \rangle ,\)  \(\vert G\rangle =\Delta B\vert \Psi \rangle\) and \(\vert \Psi \rangle\) being an arbitrary state of a system that,

Since the non-Hermitian quantum Fisher information \(F_{nH}\) benefits from mixed states, we will focus on encoding the unknown parameter into mixed states in the undergoing example. Without loss of generality, we consider a type of simplest mixed states—there are only two eigenstates and the corresponding eigenvalues are \(p_1\) and \(p_2,\) respectively, where \(p_1+p_2=1\).

For mixed states of form \(\rho =\sum _{i=1}^2 p_i\vert \phi _i\rangle \langle \phi _i\vert\) with \(\theta\)-independent \(p_i\), the Hermitian quantum Fisher information \(F_H\) [50,51,52] and non-Hermitian quantum Fisher information \(F_{nH}\) reduce to,

\(\begin{aligned} F_H= & {} \sum _{i=1}^2 \left( 4p_i\langle \partial _\theta \phi _i\vert \partial _\theta \phi _i\rangle -4p_i\vert \langle \phi _i\vert \partial _\theta \phi _i\rangle \vert ^2\right) -16p_1p_2\vert \langle \phi _1\vert \partial _\theta \phi _2\rangle \vert ^2,\nonumber \\ F_{nH}= & {} \sum _{i=1}^2 \left( p_i\langle \partial _\theta \phi _i\vert \partial _\theta \phi _i\rangle -p_i\vert \langle \phi _i\vert \partial _\theta \phi _i\rangle \vert ^2\right) +\left( \frac{p_2(1-3p_1)}{p_1}+\frac{p_1(1-3p_2)}{p_2}\right) \vert \langle \phi _1\vert \partial _\theta \phi _2\rangle \vert ^2. \end{aligned}\)

(14)

Take GHZ states \(\vert \phi _{1,2}\rangle =\frac{1}{\sqrt{2}} (\vert a\rangle ^{\otimes N}\pm \vert b\rangle ^{\otimes N})\) as the two eigenstates and suppose that the parameter \(\theta\) is encoded into these states through a spin rotation defined by \(U(\theta )=e^{-i\theta J_z}\) with Hermitian signal Hamiltonian \(J_z=\sum _{j=1}^N s_z^{(j)}\), the encoding states follow,

\(\begin{aligned} \vert \phi _{1,2}(\theta )\rangle =\frac{1}{\sqrt{2}} (e^{\frac{i}{2} N\theta }\vert a\rangle ^{\otimes N}\pm e^{-\frac{i}{2} N\theta }\vert b\rangle ^{\otimes N}). \end{aligned}\)

(15)

The rotation \(U(\theta )=e^{-i\theta J_z}\) generates a relative phase \(N\theta\) between states \(\vert a\rangle ^{\otimes N}\) and \(\vert b\rangle ^{\otimes N}\). The GHZ states have been created with up to \(N=6\) \(^9Be^+\) ions [44] and \(N=14\) \(^{40}Ca^+\) ions [53] in a linear Paul trap. With these states, the encoded mixed state reads

\begin{aligned} \rho (\theta )=\sum _{i=1}^2 p_i\vert \phi _i(\theta )\rangle \langle \phi _i(\theta )\vert , \end{aligned}

and \(p_i\, (i=1,2)\) are independent of \(\theta .\)

It is easy to find that

\(\begin{aligned} \langle \partial _\theta \phi _1\vert \partial _\theta \phi _1\rangle= & {} \frac{1}{4} N^2,\nonumber \\ \langle \partial _\theta \phi _2\vert \partial _\theta \phi _2\rangle= & {} \frac{1}{4} N^2,\nonumber \\ \langle \partial _\theta \phi _1\vert \phi _1\rangle =\langle \partial _\theta \phi _2\vert \phi _2\rangle= & {} 0,\nonumber \\ \vert \langle \partial _\theta \phi _1\vert \phi _2\rangle \vert ^2= & {} \frac{1}{4} N^2. \end{aligned}\)

(16)

Collecting these results, we obtain

\(\begin{aligned} F_H= & {} (2p-1)^2N^2,\nonumber \\ F_{nH}= & {} \frac{(2p-1)^2}{4p(1-p)}N^2. \end{aligned}\)

(17)

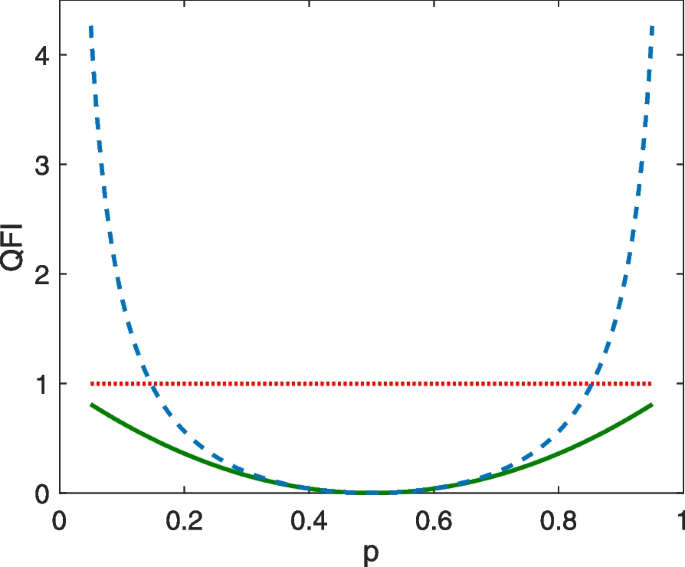
The dependance of \(F_H\) and \(F_{nH}\) are shown in Fig. 1. We find that for mixed states the non-Hermitian quantum Fisher information are always larger than the Hermitian quantum Fisher information, except the points \(p=0,0.5, 1.\) The quantum Fisher information of pure states \(F_H^p\) is larger than \(F_{nH}\) for \((2-\sqrt{2})/4. Especially, when the mixed state gets very close to pure states (\(p\rightarrow 0\) or \(p\rightarrow 1\)), \(F_{nH}\) has a very large value manifesting itself as a witness of transition from mixed states to pure states. This feature might be used to design sensors. It is worth addressing that at points \(p=0,1\), the state is pure. So, the quantum Fisher information should be calculated by the formula of pure states, which yield \(F_H=N^2\) and \(F_{nH}=0.25N^2.\) This suggests that a sensor working with mixed states very close to pure states is sensitive more than that working with pure states.

\(F_H\) (green-solid line) and \(F_{nH}\) (blue-dashed line) are Hermitian and non-Hermitian quantum Fisher information, respectively, as a function of p. p is the eigenvalue of the density matrix. The quantum Fisher information \(F_H^p\) (red-dotted line) of pure state \(\vert \phi _{1,2}(\theta )\rangle\) is also shown for comparison. All the quantum Fisher information is plotted in units of \(N^2\)

 Full size image 

The variance \((\Delta \theta )^2\) of estimation can be given by the error propagation in Eq. (3), which is bounded by the quantum Cramér-Rao bound defined through the quantum Fisher information as \((\Delta \theta )^2\ge \frac{1}{\nu F}, \quad F=F_H, \, F_{nH},\) where \(\nu\) is the number of repetitions of the experiment. Given a signal Hamiltonian and initial state, the bounds can be saturated by carefully chosen measurement described by operator A. Denoting \(A_1^{opt}\) as the optimal measurement and noticing Eqs. (4) and (8), we find that,

\(\begin{aligned} A_1^{opt}= \frac{1}{1-p}\vert \phi _1\rangle \langle \phi _2\vert -\frac{1}{p}\vert \phi _2\rangle \langle \phi _1\vert , \end{aligned}\)

(18)

where p ,  \((1-p)\) and \(\vert \phi _i\rangle\) are the eigenvalues and its corresponding eigenstates of \(\rho (\theta )\), see Eqs. (15) and (17).

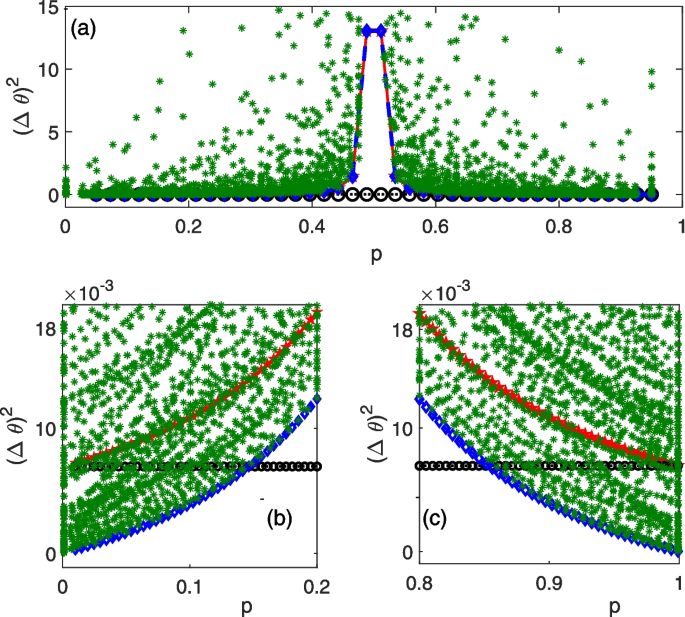
Applying this optimal measurement \(A_1^{opt}\) to \((\Delta \theta )^2=\frac{\langle \Delta A_1^{opt \dagger }\Delta A_1^{opt}\rangle }{\partial \langle A_1^{opt\dagger }\rangle /\partial \theta \cdot \partial \langle A_1^{opt}\rangle /\partial \theta }\) (see Eq. (3)) and comparing it with numerical results, we find that the operator given in Eq. (18) indeed saturate the bound \(1/F_{nH}\), see Fig. 2. With this setup, measurement of non-Hermitian operator would enhance the estimation precision for \(p<(2-\sqrt{2})/4\) or \(p>(2+\sqrt{2})/4.\) The variance approaches to zero as the encoding states tend to pure states.

Variance \((\Delta \theta )^2\) versus p, which is bounded by \(1/F_H\) (red-solid lines with pentagrams), \(1/F_{nH}\) (blue-dashed lines with squares), and \(1/F_{H}^p\) (black-dashed lines with circles). p is defined in Eq. (17). The variance (green-stars) is calculated by randomly generating operator A with Eq. (3). a, b, and c are for different range of p. The other parameter is chosen as \(N=12\)

 Full size image 

Nuclear magnetic resonance (NMR) has long been at the forefront of precision tests of fundamental physics [54, 55], including the earliest efforts to search for a parity and time-reversal violating permanent electric dipole moment of the neutron [56, 57] and recent applications in battery and sensors [58, 59].

Most recently, an experimental adiabatic quantum parameter estimation on the NMR quantum processor has been performed [60]. The authors demonstrated that with the optimized adiabatic path the precision can achieve the Heisenberg scaling. The physics behind this enhanced precision is the first order quantum phase transition and the speedup of the addibatic evolution in the sensor. This scheme possesses the advantages of easy implementation, robustness against decays, and tunable energy gaps. Here, we propose the other scheme with measuring non-Hermitian operators and encoding unknown parameters in mixed states to enhance the precision of this setup.

The effective dimensionless Hamiltonian to describe the setup can be written as [60]

\(\begin{aligned} H=-B_z \sigma _0+(1-B_z)\sigma _z+\sqrt{2}B_x\sigma _x, \end{aligned}\)

(19)

where \(B_z>0\) is the parameter to be estimated, \(B_x\) stands for the small transverse field assisting the estimation of \(B_z\), \(\sigma _0\) denotes the \(2\times 2\) identity operator, and \(\sigma _{x,z}\) are Pauli operators. The eigenstates of the effective Hamiltonian H can be written as

\begin{aligned} \vert g(B_z)\rangle= & {} -\sin \frac{\theta }{2}\vert a\rangle +\cos \frac{\theta }{2}\vert b\rangle ,\nonumber \\ \vert e(B_z)\rangle= & {} \cos \frac{\theta }{2}\vert a\rangle +\sin \frac{\theta }{2}\vert b\rangle , \end{aligned}

where \(\vert a\rangle =\vert 11\rangle\), \(\vert b\rangle =\frac{\vert 01\rangle +\vert 10\rangle }{\sqrt{2}}\) and \(\tan \theta =\frac{\sqrt{2}B_x}{1-B_z}\) [61].

The quantum Fisher information of eigenstates \(\vert g\rangle \equiv \vert g(B_z)\rangle\) and \(\vert e\rangle \equiv \vert e(B_z)\rangle\) is equal as \(\langle \partial _{B_z} g\vert \partial _{B_z} g\rangle =\langle \partial _{B_z} e\vert \partial _{B_z} e \rangle\) and \(\langle g \vert \partial _{B_z} g \rangle =\langle e \vert \partial _{B_z} e \rangle =0\). With these considerations and the use of \(F_H^p=4(\langle \partial _{B_{z}}g\vert \partial _{B_{z}}g\rangle -\vert \langle g\vert \partial _{B_{z}}g\rangle \vert ^{2})\) [60], the quantum Fisher information of eigenstates \(\vert g\rangle\) or \(\vert e\rangle\) reads,

\(\begin{aligned} F_{H}^p=\frac{2B_{x}^{2}}{[(1-B_{z})^{2}+2B_{x}^{2}]^{2}}, \end{aligned}\)

(20)

where superscript p in \(F_{H}^p\) stands for the quantum Fisher information of pure states. The key point of Ref. [60] to enhance the estimation precision is that \(F_H^p\) has a large value when \(B_x\rightarrow 0\) near the critical point \(B_z \sim 1\), and the quantum fisher information scales as \(T^2\), where T is the cost—the time required for the adiabatic evolution.

The time cost T required for the adiabatic path is determined by the adiabatic condition, which makes T long, although the shortcut to adiabaticity can solve this difficulty in some circumstances. We here propose to encode the estimation parameter \(B_z\) into mixed states,

\(\begin{aligned} \rho (B_z)=p\vert g(B_z)\rangle \langle g(B_z)\vert +(1-p)\vert e(B_z)\rangle \langle e(B_z)\vert \end{aligned}\)

(21)

with \(B_z\)-independent p. Considering \(\langle g\vert \partial _{B_z} g\rangle =\langle e\vert \partial _{B_z} e\rangle =0,\) we have

\(\begin{aligned} F_{nH}=p\langle \partial _{B_z} g\vert \partial _{B_z} g\rangle +(1-p)\langle \partial _{B_z} e\vert \partial _{B_z} e \rangle +\left( \frac{(1-p)(1-3p)}{p} + \frac{p(3p-2)}{1-p}\right) \vert \langle g\vert \partial _{B_z} e\rangle \vert ^2. \end{aligned}\)

(22)

Straightforward calculation yields,

\begin{aligned} \langle \partial _{B_z} g\vert \partial _{B_z} g\rangle =\langle \partial _{B_z} e\vert \partial _{B_z} e \rangle =\frac{1}{4} (\frac{\partial \theta }{\partial B_z})^2, \end{aligned}

and

\begin{aligned} \langle \partial _{B_z} g\vert e\rangle =\frac{1}{2} \frac{\partial \theta }{\partial B_z} \end{aligned}

with

\begin{aligned} \frac{\partial \theta }{\partial B_z}= \frac{\sqrt{2} B_x}{(1-B_z)^2+2B_x^2}. \end{aligned}

Substituting the last three equations into \(F_{nH}\), we obtain

\(\begin{aligned} F_{nH}=\frac{(2p-1)^2}{4p(1-p)}F_H^p. \end{aligned}\)

(23)

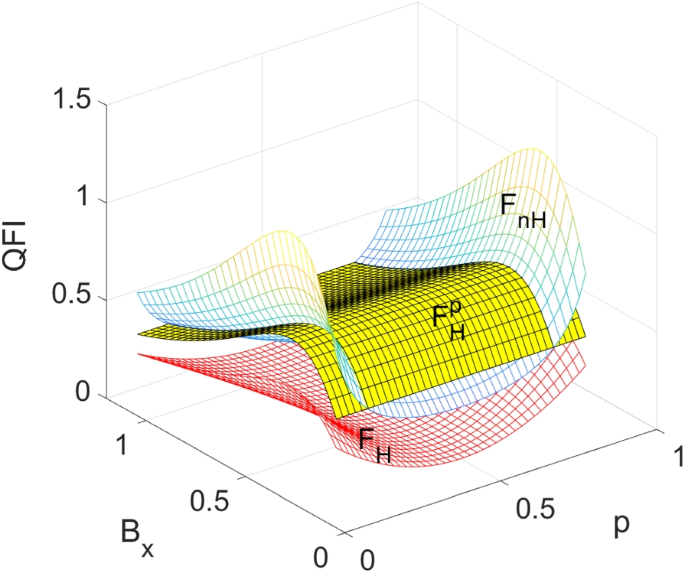
It is always larger than the Hermitian quantum Fisher information of mixed state given by \(F_{H}=(2p-1)^2F_H^p\). The dependence of quantum Fisher information on p and \(B_x\) is shown in Fig. 3. Note that \(F_{nH}>F_H\) and \(F_H^p>F_H\) holds for all p, while \(F_{nH}>F_H^p\) for \(p<\frac{1}{4}(2-\sqrt{2})\) or \(p>\frac{1}{4}(2+\sqrt{2})\). In particular, \(F_{nH}\) has a very large value when the mixed states are very close to pure states. This feature provides a scheme for parameter estimation to enhance the precision. The estimation of \(B_z\) is bounded by \(1/F_{nH}\). To saturate the bound, we need to optimize the measurement A. It is easy to find that

\(\begin{aligned} \langle g\vert L\vert g\rangle= & {} \langle e\vert L\vert e\rangle =0,\nonumber \\ \langle g\vert L\vert e\rangle= & {} \frac{1-2p}{2(1-p)}\frac{\partial \theta }{\partial B_z},\nonumber \\ \langle e\vert L\vert g\rangle= & {} \frac{1-2p}{2p}\frac{\partial \theta }{\partial B_z}. \end{aligned}\)

(24)

Thus

\(\begin{aligned} A^{opt}_2=\frac{\gamma }{2} (1-2p)\frac{\partial \theta }{\partial B_z}\left( \frac{1}{1-p}\vert g\rangle \langle e\vert + \frac{1}{p}\vert e\rangle \langle g\vert \right) . \end{aligned}\)

(25)

From the error propagation function Eq. (3), we can find that the factor \(\frac{\gamma }{2} (1-2p)\frac{\partial \theta }{\partial B_z}\) can be dropped.

\(F_H^p\) is Hermitian quantum Fisher information for pure state \(\vert g(\theta )\rangle\), and \(F_H\) and \(F_{nH}\) are Hermitian and non-Hermitian quantum Fisher information for mixed state, respectively. p is the eigenvalue of the density matrix, \(B_x\) is the amplitude of the transverse field. \(B_z=0.4\) is chosen for this plot

 Full size image 

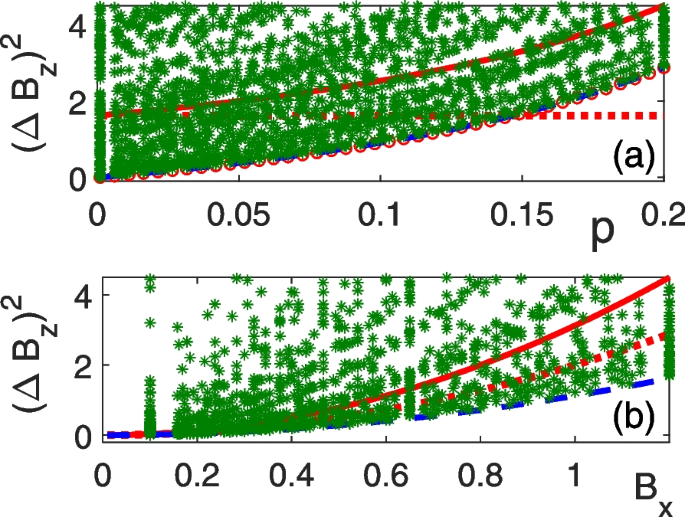
We perform numerically searching for the optimal measurement A. The result is shown in Fig. 4. We find that the variance of \(B_z\) becomes very small while p approaches to 0 as shown in Fig. 4 (a). This is reminiscent of sensors designed near quantum phase transition [60].

a, b The variance \((\Delta B_z)^2\) (green-stars) versus p and \(B_x\), respectively. The different lines are bounded by \(1/F_H\) (red-solid) and \(1/F_{nH}\) (blue-dashed) for mixed state, and \(1/F_{H}^p\) (red-solid) is for pure state. p is defined in Eq. (17). The variance \((\Delta B_z)^2\) is calculated by Eq. (3) with random variable A

 Full size image 

In the last sections, we have derived an unknown quantum Cramér-Rao bound defined by a quantum Fisher information for non-Hermitian operators and demonstrated the theory with the phase estimation of trapped ions and a setup of adiabatic quantum parameter estimation. One may wonder how to measure the non-Hermitian operators \(A_i^{opt}\, (i=1,2)\) to attain the bounds? Here, we follow the proposal in Refs. [39,40,41,42] to show it in experiment.

The expectation value of \(A_i^{opt}\,(i=1,2)\) in a quantum state \(\vert \phi _{in}\rangle\) is given by \(\langle \phi _{in}\vert A_i^{opt}\vert \phi _{in}\rangle\). It is complex in general and makes the non-Hermitian operator \(A_i^{opt}\) unobservable in experiment. Nevertheless, recent studies shown that this obstacle can be overcome with the help of polar decomposition [62]. Namely, \(A_i^{opt} = UR\) with unitary operator U and Hermitian semidefinite operator R, \(R=\sqrt{(A_i^{opt})^\dagger A_i^{opt}}.\) This connects the average of non-Hermitian operator \(A_i^{opt}\) with the weak value of Hermitian operator R as follows,

\(\begin{aligned} \langle \phi _{in} \vert A_i^{opt}\vert \phi _{in}\rangle =\langle \phi _{in} \vert UR\vert \phi _{in}\rangle = \frac{\langle \phi \vert R\vert \phi _{in}\rangle }{\langle \phi \vert \phi _{in}\rangle }\langle \phi \vert \phi _{in}\rangle , \end{aligned}\)

(26)

where \(\langle \phi \vert \equiv \langle \phi _{in} \vert U.\) It is well-known that \(\frac{\langle \phi \vert R\vert \phi _{in}\rangle }{\langle \phi \vert \phi _{in}\rangle }\) is a weak value of the positive-semidefinite operator R, which can be measured directly in the weak measurement with successful probability depending on the post- and pre-selection states [63]. However, there are other approaches to obtain the weak value via the weak measurement [40, 41] without post-selection [42] in experiment. And the measurement of non-Hermitian operator can be implemented with an interferometric technique [41]. The average of the non-Hermitian operator can be determined through the intensity measured by a detector at the output without post-selection, so that there are no concerns of successful probability. Next, before going into details of such a technique, we first find R and U to decompose the non-Hermitian operator \(A^{opt}=UR\).

To be specific, let us consider the optimal operator \(A_2^{opt}\) given in Eq. (25). Straightforward derivation yields,

\(\begin{aligned} R= & {} \frac{1}{p} \vert g\rangle \langle g\vert +\frac{1}{1-p}\vert e\rangle \langle e\vert ,\nonumber \\ U= & {} \vert e\rangle \langle g\vert +\vert g\rangle \langle e\vert . \end{aligned}\)

(27)

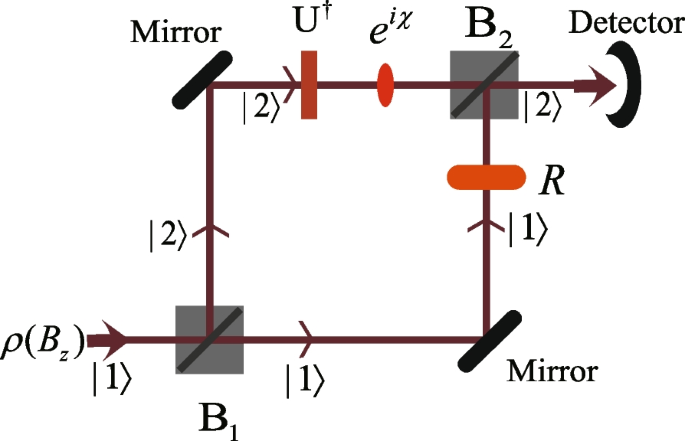
R can be rewritten as a project operator, \(R=\frac{1}{p} (\sigma _0+\frac{2p-1}{1-p}\vert e\rangle \langle e\vert )\), and U can be treated as a beam splitter. Both Hermitian operator R and unitary operator U depend on \(B_z\) and can be realized in experiments with the established \(B_z\) based on prior data [60, 64]. \(\sigma _0\) is the \(2\times 2\) identity operator. The schematic setup to measure the average of \(A_2^{opt}\) on state \(\rho (B_z)\) is illustrate in Fig. 5.

Schematic setup to measure \(A^{opt}_2=UR\) on state \(\rho (B_z)\). \(B_1\) and \(B_2\) are 50:50 Hadamard-type beam splitters, which split the spatial modes representing by \(\vert 1\rangle\) and \(\vert 2\rangle\). \(e^{i\chi }\) is a phase shifter that introduces a relative phase \(\chi\) between the two arms. We measure the intensity at the detector as a function of \(\chi\) and the value of \(\text {Tr}(\rho (B_z)A_2^{opt})\) would be read out from the intensity of the output

 Full size image 

To simplify the notation, we write \(\vert g\rangle =\vert g(B_z)\rangle\) and \(\vert e\rangle =\vert e(B_z)\rangle\). To measure \(A^{opt}_2\), we first show that the average of \(A^{opt}_2\) in pure state \(\vert g\rangle\), \(\langle g\vert A^{opt}_2 \vert g\rangle \equiv \vert A^{opt}_2 \vert e^{i\zeta _g}\) can be readout from the intensity measured by the detector. Then, we extend this result to mixed state \(\rho (B_z) = p\vert g\rangle \langle g\vert +(1-p)\vert e\rangle \langle e\vert .\) Namely, the average of \(A^{opt}_2\) on state \(\rho (B_z)\) can be read out from the intensity at the detector too.

In bases spanned by \(\vert a,1\rangle , \vert b,1\rangle ,\vert a,2\rangle , \vert b,2\rangle\) (\(\vert x,n\rangle \equiv \vert x\rangle \otimes \vert n\rangle , x=a,b; n=1,2\)) [65], these operation \(B_i (i=1 ,2), R, U^\dagger , e^{i\chi }\) can be represented by [47],

\(\begin{aligned} B_{1,2}= \frac{1}{\sqrt{2}}\left( \begin{array}{cccc} 1 &{} 0 &{} i &{}0 \\ 0 &{} 1 &{} 0 &{}i \\ i &{} 0 &{} 1 &{}0 \\ 0 &{} i &{} 0 &{}1 \\ \end{array}\right) , R= \left( \begin{array}{cccc} R_{aa} &{} R_{ab} &{} 0 &{}0 \\ R_{ba} &{} R_{bb} &{} 0 &{}0 \\ 0 &{} 0 &{} 1 &{}0 \\ 0 &{} 0 &{} 0 &{}1 \\ \end{array}\right) , e^{i\chi }= \left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{}0 \\ 0 &{} 1 &{} 0 &{}0 \\ 0 &{} 0 &{} e^{i\chi } &{}0 \\ 0 &{} 0 &{} 0 &{}e^{i\chi } \\ \end{array}\right) , U^\dagger = \left( \begin{array}{cccc} 1 &{}0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} U^\dagger _{aa} &{} U^\dagger _{ab}\\ 0 &{} 0 &{} U^\dagger _{ba} &{} U^\dagger _{bb}\\ \end{array}\right) , \end{aligned}\)

(28)

where \(R_{ab}=\langle a\vert R\vert b\rangle\), and similar notations hold for \(R_{aa}, R_{bb}, R_{ba}\) and \(U^\dagger _{xy}, x,y=a,b\). The input state that only occupies spatial state \(\vert 1\rangle\) can be written as,

\(\begin{aligned} \vert g\rangle= & {} \left( \begin{array}{c} \phi _{a}\\ \phi _{b}\\ 0\\ 0\\ \end{array}\right) , \phi _a\equiv \langle a\vert g\rangle , \, \phi _b\equiv \langle b\vert g\rangle . \end{aligned}\)

(29)

The output state reads

\(\begin{aligned} \vert \phi _{out}\rangle = B_2 e^{i\chi } U^\dagger R B_1\vert g\rangle . \end{aligned}\)

(30)

Simple algebra yields,

\begin{aligned} \vert \phi _{out}\rangle&=\frac{1}{2}&\left( \begin{array}{c} R_{aa}\phi _a+R_{ab}\phi _b-(U^\dagger _{aa}\phi _a+U^\dagger _{ab}\phi _b)e^{i\chi } \\ R_{ba}\phi _a+R_{bb}\phi _b-(U^\dagger _{ba}\phi _a+U^\dagger _{bb}\phi _b)e^{i\chi } \\ i[R_{aa}\phi _a+R_{ab}\phi _b+(U^\dagger _{aa}\phi _a+U^\dagger _{ab}\phi _b)e^{i\chi }] \\ i[R_{ba}\phi _a+R_{bb}\phi _b+(U^\dagger _{ba}\phi _a+U^\dagger _{bb}\phi _b)e^{i\chi }] \\ \end{array}\right) . \end{aligned}

The intensity the detector measures can be represented by

\(\begin{aligned} I_g(\chi )=\vert \langle \phi _D\vert \phi _D\rangle \vert ^2, \quad \vert \phi _D\rangle \equiv D \vert \phi _{out}\rangle , \end{aligned}\)

(31)

with

\(\begin{aligned} D= \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 0 &{} 1 &{}0 \\ 0 &{} 0 &{} 0 &{}1 \\ \end{array}\right) , \end{aligned}\)

(32)

leading to

\(\begin{aligned} I_g(\chi )=\frac{1}{4} \left( \frac{}{}1+\langle g\vert R^2\vert g\rangle +2\vert \langle g\vert A^{opt}_2 \vert g\rangle \vert \cos (\chi -\zeta _g)\right) , \end{aligned}\)

(33)

where \(\zeta _g\) is the argument of \(\langle g\vert A^{opt}_2 \vert g\rangle\), i.e., \(\zeta _g=\arg \langle g\vert A^{opt}_2 \vert g\rangle .\)

To measure the average of \(A^{opt}_2\) on mixed state \(\rho (B_z)=p\vert g\rangle \langle g\vert +(1-p)\vert e\rangle \langle e\vert ,\) we replace the input state \(\vert g\rangle\) by \(\rho (B_z)\). The output state is then,

\(\begin{aligned} \rho _{out}=p Q \vert g\rangle \langle g\vert Q ^{\dagger }+(1-p) Q \vert e\rangle \langle e\vert Q ^{\dagger }, \end{aligned}\)

(34)

where \(Q =DB_2e^{i\chi }U^{\dagger }RB_1\). The intensity that the detector measures is

\(\begin{aligned} I(\chi )=\vert \text {Tr}(\rho _{out})\vert ^2=pI_g(\chi )+(1-p)I_e(\chi ), \end{aligned}\)

(35)

where \(I_g(\chi )=\vert \langle g\vert Q ^\dagger Q \vert g\rangle \vert ^2\) and \(I_e(\chi )=\vert \langle e\vert Q ^\dagger Q \vert e\rangle \vert ^2.\) Substituting Q into \(I_x\) (\(x=g,e\)), we find

\begin{aligned} I_x(\chi )=1+\langle x\vert R^2\vert x\rangle +2\vert \langle x\vert A_2^{opt}\vert x\rangle \vert \cos (\chi -\zeta _x), \end{aligned}

and \(\langle x\vert A_2^{opt}\vert x\rangle =\vert \langle x\vert A_2^{opt}\vert x\rangle \vert e^{i\zeta _x}.\) In experimental implementations, the intensity \(I(\chi )\) together with \(\langle x\vert R^2\vert x\rangle\) (the average of Hermitian operator \(R^2\) on state \(\vert x\rangle\)) can determine the average of non-Hermitian operator \(A_2^{opt},\) as both \(\vert \langle x\vert A\vert x\rangle \vert\) and \(\zeta _x\) can be inferred from the intensity \(I(\chi )\).

The framework of quantum mechanics in which observables are associated only with Hermitian operators constrains the optimization in quantum parameter estimation. Considering the fact that in the past two decades the non-Hermitian physics has attracted fast growing interest in various research field, we have extended measurements from Hermitian operators to all operators including non-Hermitian ones. With this extension, a previously unknown expression for quantum Fisher information has been derived and a new quantum Cramér-Rao bound has been established. The saturation of the bound has been analyzed and the optimal measurement to attain the bounds have been given. The theory was elucidated with two experimentally feasible systems. In the example of phase estimation, we find that mixed states can further enhance the sensitivity of phase estimation with measurements of non-Hermitian operators. While in the example of adiabatic quantum parameter estimation for the estimation of magnetic fields on a nuclear magnetic resonance, the variance of the magnetic field under estimation can reach arbitrary small values depending on the encoding states. A setup to measure non-Hermitian operator was also proposed.